题目内容
(本小题满分14分)
如图,设抛物线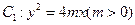 的准线与
的准线与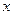 轴交于
轴交于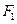 ,焦点为
,焦点为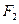 ;以
;以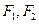 为焦点,离心率
为焦点,离心率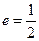 的椭圆
的椭圆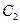 与抛物线
与抛物线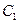 在
在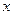 轴上方的交点为
轴上方的交点为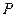 ,延长
,延长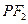 交抛物线于点
交抛物线于点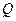 ,
,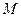 是抛物线
是抛物线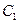 上一动点,且M在
上一动点,且M在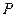 与
与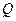 之间运动.
之间运动.
(1)当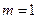 时,求椭圆
时,求椭圆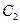 的方程,
的方程,
(2)当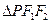 的边长恰好是三个连续的自然数时,
的边长恰好是三个连续的自然数时,
求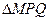 面积的最大值.
面积的最大值.
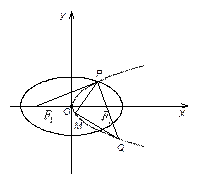
如图,设抛物线
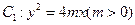 的准线与
的准线与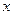 轴交于
轴交于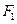 ,焦点为
,焦点为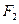 ;以
;以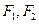 为焦点,离心率
为焦点,离心率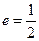 的椭圆
的椭圆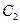 与抛物线
与抛物线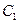 在
在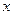 轴上方的交点为
轴上方的交点为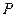 ,延长
,延长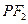 交抛物线于点
交抛物线于点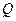 ,
,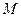 是抛物线
是抛物线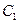 上一动点,且M在
上一动点,且M在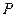 与
与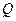 之间运动.
之间运动.(1)当
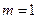 时,求椭圆
时,求椭圆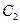 的方程,
的方程,(2)当
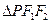 的边长恰好是三个连续的自然数时,
的边长恰好是三个连续的自然数时,求
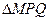 面积的最大值.
面积的最大值.
(1)
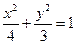
(2)
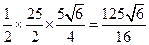
解:(1)当
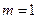 时,
时,
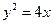 ,则
,则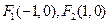
设椭圆方程
 为
为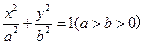 ,则
,则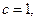 又
又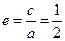 ,所以
,所以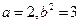
所以椭圆C2方程为
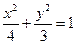 …………4分
…………4分(2)因为
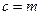 ,
,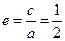 ,则
,则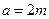 ,
, ,设椭圆方程为
,设椭圆方程为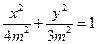
由
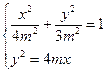 ,得
,得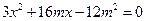 …………6分
…………6分即
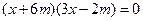 ,得
,得 代入抛物线方程得
代入抛物线方程得 ,即
,即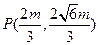
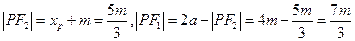 ,
,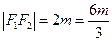 ,
, 即
即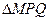 面积的最大值为
面积的最大值为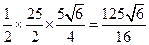 . …………14分
. …………14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
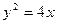 ,过
,过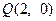 作直线
作直线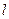 .
.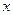 轴不垂直,交抛物线于A、B两点,是否存在
轴不垂直,交抛物线于A、B两点,是否存在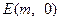 ,使得
,使得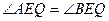 ?若存在,求出m的值;若不存在,请说
?若存在,求出m的值;若不存在,请说 明理由?
明理由?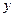 轴和
轴和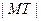 为定值,试证之;
为定值,试证之;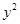 =2x的焦点为F,过点M(
=2x的焦点为F,过点M(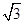 ,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,
,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,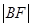 =2,则
=2,则
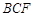 与
与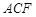 的面积之比
的面积之比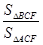 =( )
=( )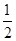
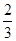
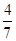
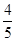
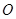 和点
和点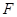 分别是抛物线
分别是抛物线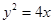 的顶点和焦点,点
的顶点和焦点,点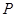 为抛物线上的任意一点,则
为抛物线上的任意一点,则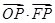 的取值范围为 ( *** )
的取值范围为 ( *** )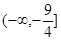
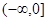
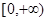
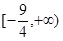
 轴上的抛物线与直线
轴上的抛物线与直线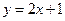 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|=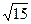 ,求抛物线的方程
,求抛物线的方程
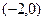 ,则抛物线的标准方程是 .
,则抛物线的标准方程是 . 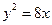 上一点P到y轴的距离是4,
上一点P到y轴的距离是4, 则点P到该抛物线焦点的距离是( )
则点P到该抛物线焦点的距离是( )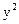 =–x与直线y="k(x" + 1)相交于A、B两点,则△AOB的形状是
=–x与直线y="k(x" + 1)相交于A、B两点,则△AOB的形状是 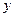 轴,焦点在直线
轴,焦点在直线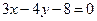 上的抛物线的标准方程是
上的抛物线的标准方程是