题目内容
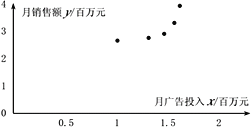
【题目】长沙某公司对其主推产品在过去5个月的月广告投入xi(百万元)和相应的销售额yi(百万元)进行了统计,其中i=1,2,3,4,5,对所得数据进行整理,绘制散点图并计算出一些统计量如下:
|
|
|
|
|
|
|
68 | 10.3 | 15.8 | -192.12 | 1.602 | 0.46 | 3.56 |
其中![]() ,i=1,2,3,4,5.
,i=1,2,3,4,5.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为月销售额关于月广告投入xi的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为月销售额关于月广告投入xi的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及题中所给数据,建立y关于x的回归方程,并据此估计月广告投入200万元时的月销售额.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: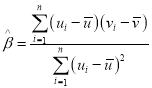 ,
,![]() .
.
【答案】(1)选择![]() ;(2)
;(2)![]() ,
,![]() 百万元.
百万元.
【解析】
(1)根据散点的分布情况以及一次函数,二次函数的图象可知,应选择![]() 作为回归方程;
作为回归方程;
(2)通过换元,令![]() ,将非线性回归模型转化为线性回归模型,再根据题目所给的数据利用最小二乘法即可求出线性回归方程,进而得到y关于x的回归方程,然后将
,将非线性回归模型转化为线性回归模型,再根据题目所给的数据利用最小二乘法即可求出线性回归方程,进而得到y关于x的回归方程,然后将![]() 代入,即可估计月广告投入2百万元时的月销售额.
代入,即可估计月广告投入2百万元时的月销售额.
(1)根据散点图选择![]() 作为回归方程.
作为回归方程.
(2)令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
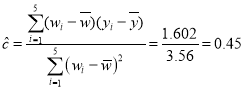 ,
,![]() ,
,
故回归方程为![]() ,
,
当月广告投入为2百万元时,月销售额为![]() (百万元).
(百万元).
答:选择![]() 作为回归方程,当月广告投入为2百万元时,月销售额约
作为回归方程,当月广告投入为2百万元时,月销售额约![]() 百万元.
百万元.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】体育测试成绩分为四个等级:优、良、中、不及格.某班50名学生参加测试结果如下:
等级 | 优(86~100分) | 良(75~85分) | 中(60~74分) | 不及格(1~59分) |
人数 | 5 | 21 | 22 | 2 |
(1)估计该班学生体育测试的平均成绩;
(2)从该班任意抽取1名学生,求这名学生的测试成绩为“优”或“良”的概率.