题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 在
在![]() 上的最小值;
上的最小值;
(2)求函数![]() 在
在![]() 上的最小值;
上的最小值;
(3)求函数![]() 在
在![]() 上的值域.
上的值域.
【答案】(1)![]() ;(2)
;(2)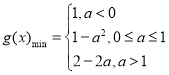 ;(3)当
;(3)当![]() 时,
时,![]() 值域为
值域为![]() ,
,![]() 时,
时,![]() 值域为
值域为![]() ,当
,当![]() 时,
时,![]() 值域为
值域为![]() ,
,![]() 时
时![]() 值域为
值域为![]() ,
,![]() 时
时![]() 值域为
值域为![]() ,
,![]() 时
时![]() 值域为
值域为![]() .
.
【解析】
(1)确定![]() 在
在![]() 上的单调性,然后可得最小值;
上的单调性,然后可得最小值;
(2)分类讨论,根据对称轴与区间![]() 关系分类;
关系分类;
(3)根据复合函数的单调性分类求解.注意函数的定义域.
(1)![]()
![]() ,函数在
,函数在![]() 上单调递减,∴
上单调递减,∴![]() ;
;
(2)![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
综上 .
.
(3)![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 时,
时,![]() 时,
时,![]() 值域为
值域为![]() ,
,![]() 时,
时,![]() 值域为
值域为![]() ,当
,当![]() 时,
时,![]() 值域为
值域为![]() ,
,![]() 时,
时,![]() 的值域是
的值域是![]() ,
,
由(1)![]() 在
在![]() 和
和![]() 上都是递减,
上都是递减,
显然当![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() 值域为
值域为![]() ,
,![]() 时,
时,![]() 值域为
值域为![]() ,当
,当![]() 时,
时,![]() 值域为
值域为![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 值域为
值域为![]() ,
,
![]() 时,
时,![]() ,取
,取![]() ,
,![]() 值域为
值域为![]() ,
,
当![]() 时,
时,![]() ,取
,取![]() 和
和![]() ,
,![]() 值域为
值域为![]() .
.
综上,当![]() 时,
时,![]() 值域为
值域为![]() ,
,![]() 时,
时,![]() 值域为
值域为![]() ,当
,当![]() 时,
时,![]() 值域为
值域为![]() ,
,![]() 时
时![]() 值域为
值域为![]() ,
,![]() 时
时![]() 值域为
值域为![]() ,
,![]() 时
时![]() 值域为
值域为![]() .
.

练习册系列答案
相关题目
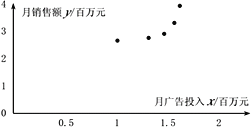
【题目】长沙某公司对其主推产品在过去5个月的月广告投入xi(百万元)和相应的销售额yi(百万元)进行了统计,其中i=1,2,3,4,5,对所得数据进行整理,绘制散点图并计算出一些统计量如下:
|
|
|
|
|
|
|
68 | 10.3 | 15.8 | -192.12 | 1.602 | 0.46 | 3.56 |
其中![]() ,i=1,2,3,4,5.
,i=1,2,3,4,5.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为月销售额关于月广告投入xi的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为月销售额关于月广告投入xi的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及题中所给数据,建立y关于x的回归方程,并据此估计月广告投入200万元时的月销售额.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: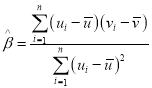 ,
,![]() .
.