题目内容
已知双曲线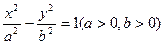 的离心率e=2,且
的离心率e=2,且 、
、 分别是双曲线虚轴的上、下端点
分别是双曲线虚轴的上、下端点
(Ⅰ)若双曲线过点 (
( ,
,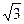 ),求双曲线的方程;
),求双曲线的方程;
(Ⅱ)在(Ⅰ)的条件下,若 、
、 是双曲线上不同的两点,且
是双曲线上不同的两点,且 ,求直线
,求直线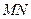 的方程
的方程
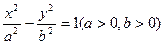 的离心率e=2,且
的离心率e=2,且 、
、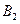 分别是双曲线虚轴的上、下端点
分别是双曲线虚轴的上、下端点
(Ⅰ)若双曲线过点
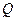 (
( ,
,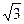 ),求双曲线的方程;
),求双曲线的方程;(Ⅱ)在(Ⅰ)的条件下,若
 、
、 是双曲线上不同的两点,且
是双曲线上不同的两点,且 ,求直线
,求直线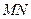 的方程
的方程
(Ⅰ)双曲线方程为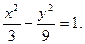
(Ⅱ)直线 的方程为
的方程为 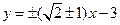
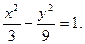
(Ⅱ)直线
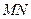 的方程为
的方程为 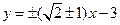
(Ⅰ)∵双曲线方程为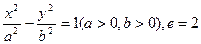
 ∴
∴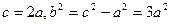 ,
,
∴双曲线方程为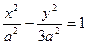 ,又曲线C过点Q(2,
,又曲线C过点Q(2,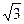 ),
),
∴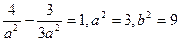
∴双曲线方程为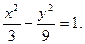 ………………5分
………………5分
(Ⅱ)∵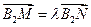 ,∴M、B2、N三点共线
,∴M、B2、N三点共线
∵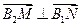 , ∴
, ∴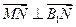
(1)当直线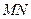 垂直x轴时,不合题意
垂直x轴时,不合题意
(2)当直线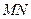 不垂直x轴时,由B1(0,3),B2(0,-3),
不垂直x轴时,由B1(0,3),B2(0,-3),
可设直线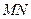 的方程为
的方程为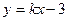 ,①
,①
∴直线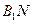 的方程为
的方程为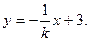 ②
②
由①,②知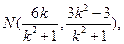 代入双曲线方程得
代入双曲线方程得
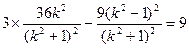 ,得
,得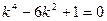 ,
,
解得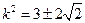 , ∴
, ∴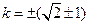 ,
,
故直线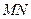 的方程为
的方程为 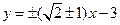
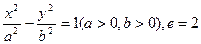
 ∴
∴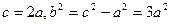 ,
,∴双曲线方程为
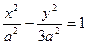 ,又曲线C过点Q(2,
,又曲线C过点Q(2,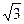 ),
),∴
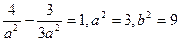
∴双曲线方程为
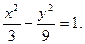 ………………5分
………………5分(Ⅱ)∵
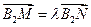 ,∴M、B2、N三点共线
,∴M、B2、N三点共线
∵
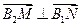 , ∴
, ∴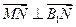
(1)当直线
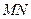 垂直x轴时,不合题意
垂直x轴时,不合题意
(2)当直线
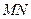 不垂直x轴时,由B1(0,3),B2(0,-3),
不垂直x轴时,由B1(0,3),B2(0,-3),可设直线
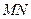 的方程为
的方程为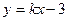 ,①
,①∴直线
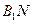 的方程为
的方程为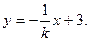 ②
②由①,②知
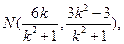 代入双曲线方程得
代入双曲线方程得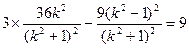 ,得
,得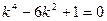 ,
,解得
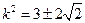 , ∴
, ∴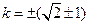 ,
,故直线
 的方程为
的方程为 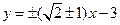

练习册系列答案
相关题目
 轴上的双曲线
轴上的双曲线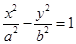 的右准线与两条渐近线交于
的右准线与两条渐近线交于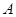 、
、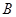 两点,右焦点为
两点,右焦点为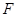 ,且
,且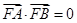 ,则双曲线的离心率
,则双曲线的离心率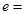 .
.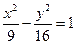 的右顶点为A,右焦点为F,过点F平行双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为 。
的右顶点为A,右焦点为F,过点F平行双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为 。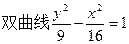 的两个焦点,M是双曲线上一点,且
的两个焦点,M是双曲线上一点,且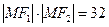 ,求三角形△F1MF2的面积
,求三角形△F1MF2的面积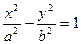 (a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和s≥
(a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和s≥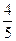 c.求双曲线的离心率e的取值范围.
c.求双曲线的离心率e的取值范围.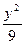 -
-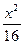 =-1上的点M到点A(5,0)的距离为25,则M到点B(-5,0)的距离是___________________.
=-1上的点M到点A(5,0)的距离为25,则M到点B(-5,0)的距离是___________________.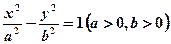 的离心率是2,则
的离心率是2,则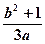 的最小值为( )
的最小值为( )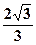
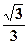
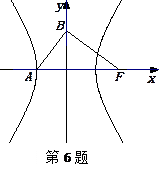 如图,双曲线
如图,双曲线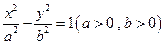 中,
中, 为右焦点,
为右焦点, 为左顶点,点
为左顶点,点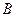 的坐标为
的坐标为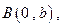 若
若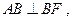 则此双曲线的离心率为 ( )
则此双曲线的离心率为 ( )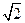
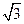
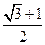
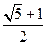
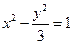 的左顶点为
的左顶点为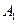 ,右焦点为
,右焦点为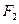 ,
,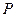 为双曲线右支上一点,则
为双曲线右支上一点,则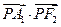 最小值为 。
最小值为 。