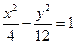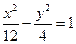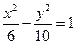题目内容
设焦点在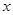 轴上的双曲线
轴上的双曲线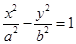 的右准线与两条渐近线交于
的右准线与两条渐近线交于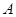 、
、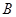 两点,右焦点为
两点,右焦点为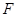 ,且
,且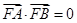 ,则双曲线的离心率
,则双曲线的离心率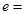 .
.
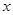 轴上的双曲线
轴上的双曲线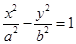 的右准线与两条渐近线交于
的右准线与两条渐近线交于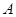 、
、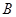 两点,右焦点为
两点,右焦点为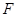 ,且
,且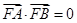 ,则双曲线的离心率
,则双曲线的离心率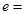 .
.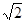
先求出A、B两点及右焦点F的坐标,由 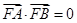 及c2=a2+b2,找出a、c的关系,从而求出离心率.
及c2=a2+b2,找出a、c的关系,从而求出离心率.
解:∵双曲线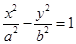 的右准线与两条渐近线交于A、B两点,右焦点为F,
的右准线与两条渐近线交于A、B两点,右焦点为F,
∴A(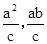 )、B(
)、B(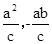 ),F(c,0),
),F(c,0),
∵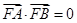 ,∴(
,∴(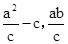 )?(
)?(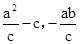 )=0,
)=0,
又c2=a2+b2,∴(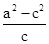 )2=
)2=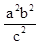 ,∴
,∴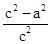 =
=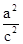 ,
,
c2=2a2,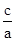 =
=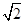 ;
;
故答案为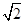 .
.
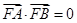 及c2=a2+b2,找出a、c的关系,从而求出离心率.
及c2=a2+b2,找出a、c的关系,从而求出离心率.解:∵双曲线
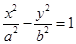 的右准线与两条渐近线交于A、B两点,右焦点为F,
的右准线与两条渐近线交于A、B两点,右焦点为F,∴A(
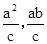 )、B(
)、B(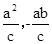 ),F(c,0),
),F(c,0),∵
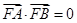 ,∴(
,∴(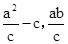 )?(
)?(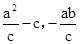 )=0,
)=0,又c2=a2+b2,∴(
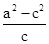 )2=
)2=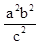 ,∴
,∴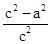 =
=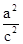 ,
,c2=2a2,
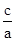 =
=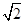 ;
;故答案为
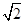 .
.
练习册系列答案
相关题目
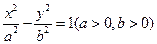 的左、右焦点分别为
的左、右焦点分别为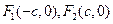 ,若双曲线上存在一点
,若双曲线上存在一点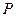 使
使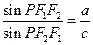 ,则该双曲线的离心率的取值范围是 。
,则该双曲线的离心率的取值范围是 。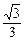


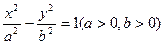 的离心率e=2,且
的离心率e=2,且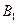 、
、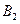 分别是双曲线虚轴的上、下端点
分别是双曲线虚轴的上、下端点
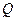 (
( ,
,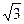 ),求双曲线的方程;
),求双曲线的方程; 、
、 是双曲线上不同的两点,且
是双曲线上不同的两点,且 ,求直线
,求直线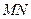 的方程
的方程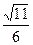 ,且C′的焦距是2
,且C′的焦距是2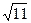 ,则此双曲线的方程为__________________.
,则此双曲线的方程为__________________.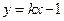 与双曲线
与双曲线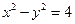 仅有一个公共点,则满足条件的实数
仅有一个公共点,则满足条件的实数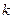
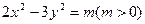 ,此双曲线的离心率为
,此双曲线的离心率为
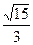
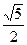
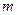 的值有关
的值有关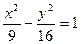 有共同的渐近线,并且过点A(
有共同的渐近线,并且过点A(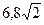 )的双曲线的标准方程为________________________.
)的双曲线的标准方程为________________________.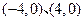 ,则双曲线的方程为
,则双曲线的方程为