题目内容
((本题满分15分)长为3的线段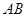 的两个端点
的两个端点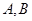 分别在
分别在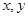 轴上移动,点
轴上移动,点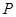 在直线
在直线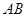 上且满足
上且满足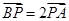 .(I)求点
.(I)求点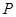 的轨迹的方程;(II)记点
的轨迹的方程;(II)记点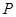 轨迹为曲线
轨迹为曲线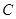 ,过点
,过点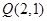 任作直线
任作直线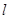 交曲线
交曲线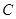 于
于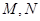 两点,过
两点,过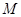 作斜率为
作斜率为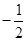 的直线
的直线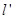 交曲线
交曲线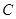 于另一点
于另一点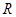 .求证:直线
.求证:直线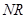 与直线
与直线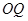 的交点为定点(
的交点为定点(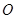 为坐标原点),并求出该定点.
为坐标原点),并求出该定点.
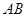 的两个端点
的两个端点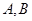 分别在
分别在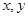 轴上移动,点
轴上移动,点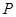 在直线
在直线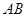 上且满足
上且满足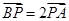 .(I)求点
.(I)求点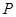 的轨迹的方程;(II)记点
的轨迹的方程;(II)记点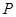 轨迹为曲线
轨迹为曲线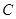 ,过点
,过点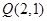 任作直线
任作直线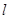 交曲线
交曲线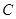 于
于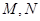 两点,过
两点,过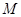 作斜率为
作斜率为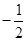 的直线
的直线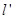 交曲线
交曲线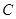 于另一点
于另一点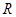 .求证:直线
.求证:直线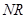 与直线
与直线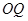 的交点为定点(
的交点为定点(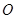 为坐标原点),并求出该定点.
为坐标原点),并求出该定点.解:(I)设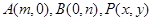
由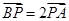 得
得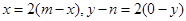 即
即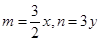
又由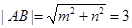 得
得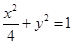 即为点
即为点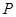 的轨迹方程.……5分
的轨迹方程.……5分
(II)当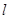 的斜率不存在时,直线
的斜率不存在时,直线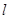 与曲线
与曲线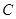 相切,不合题意;
相切,不合题意;
当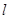 斜率存在时,设直线
斜率存在时,设直线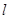 的方程为
的方程为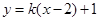 ,即
,即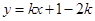
联列方程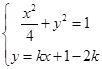 得
得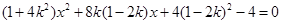
设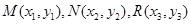 ,
,
则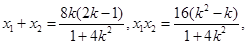 ……………7分
……………7分
则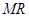 的方程为
的方程为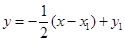
与曲线C的方程联列得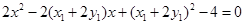
则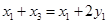
所以 ……………9分
……………9分
直线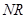 的方程为
的方程为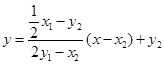
令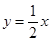 ,则
,则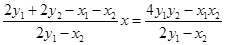
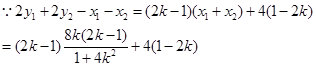
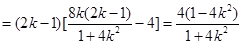 .………………………11分
.………………………11分
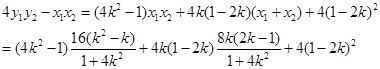
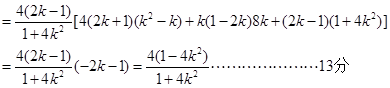
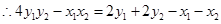 .
.
从而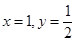 .即直线
.即直线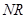 与直线
与直线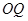 交于定点
交于定点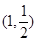 .………15分
.………15分
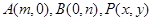
由
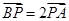 得
得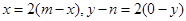 即
即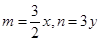
又由
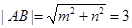 得
得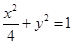 即为点
即为点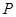 的轨迹方程.……5分
的轨迹方程.……5分(II)当
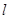 的斜率不存在时,直线
的斜率不存在时,直线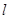 与曲线
与曲线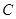 相切,不合题意;
相切,不合题意;当
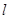 斜率存在时,设直线
斜率存在时,设直线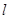 的方程为
的方程为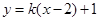 ,即
,即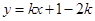
联列方程
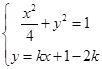 得
得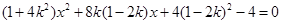
设
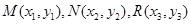 ,
,则
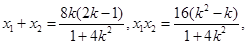 ……………7分
……………7分则
 的方程为
的方程为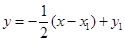
与曲线C的方程联列得
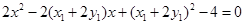
则
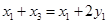
所以
 ……………9分
……………9分直线
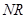 的方程为
的方程为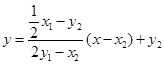
令
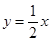 ,则
,则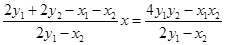
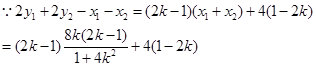
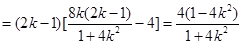 .………………………11分
.………………………11分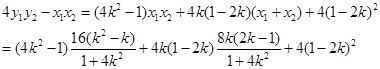
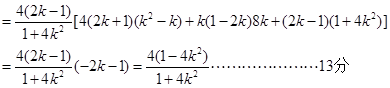
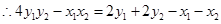 .
.从而
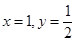 .即直线
.即直线 与直线
与直线 交于定点
交于定点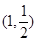 .………15分
.………15分略

练习册系列答案
相关题目
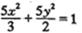
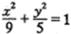
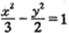

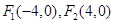 又
又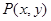 是曲线
是曲线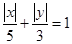 上的点,则( )
上的点,则( )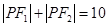
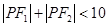
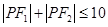
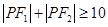
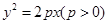 的焦点,斜率为
的焦点,斜率为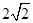 的直线交抛物线于
的直线交抛物线于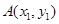 ,
,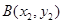
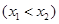 两点,且
两点,且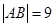 .
.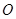 为坐标原点,是否存在平行于
为坐标原点,是否存在平行于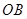 的直线
的直线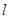 ,使得直线
,使得直线 直线
直线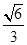 ?若存在,求出直线
?若存在,求出直线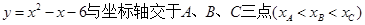 ,圆
,圆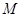 为
为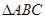 的外接圆,斜率为1的直线
的外接圆,斜率为1的直线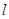 与圆
与圆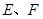 ,
,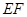 的中点为
的中点为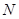 ,
,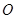 为坐标原点,且
为坐标原点,且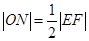 .
.
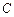 :
: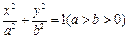 的离心率为
的离心率为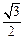 ,且过
,且过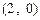 点.⑴求椭圆
点.⑴求椭圆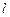 :
: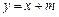 与椭圆
与椭圆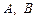 两点,
两点,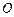 为坐标原点,若
为坐标原点,若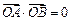 ,求
,求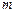 的值。
的值。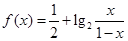 的图象上任两点,且
的图象上任两点,且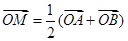 ,已知点M横坐标为
,已知点M横坐标为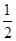 ,
,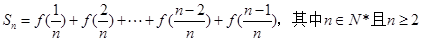 ,求Sn。
,求Sn。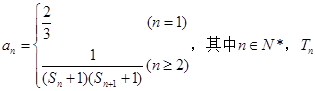 为数列{an}的前n项和, 若
为数列{an}的前n项和, 若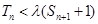 对一切
对一切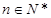 都成立,求
都成立,求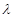 取值范围。
取值范围。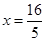 的距离的比是
的距离的比是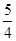 ,求P点的轨迹方程,并画出轨迹示意图。
,求P点的轨迹方程,并画出轨迹示意图。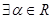 ,使得
,使得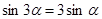 ; ②
; ②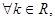 曲线
曲线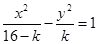 表示双曲线;
表示双曲线;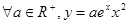 的递减区间为
的递减区间为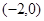 ④
④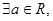 对
对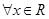 ,使得
,使得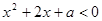 其中真命题为 (填上序号)
其中真命题为 (填上序号)