题目内容
已知过抛物线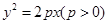 的焦点,斜率为
的焦点,斜率为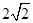 的直线交抛物线于
的直线交抛物线于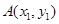 ,
,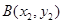
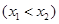 两点,且
两点,且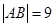 .
.
(1)求该抛物线的方程;
(2)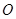 为坐标原点,是否存在平行于
为坐标原点,是否存在平行于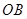 的直线
的直线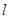 ,使得直线
,使得直线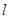 与抛物线有公共点,且
与抛物线有公共点,且 直线
直线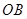 与
与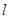 的距离为
的距离为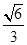 ?若存在,求出直线
?若存在,求出直线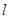 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
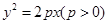 的焦点,斜率为
的焦点,斜率为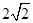 的直线交抛物线于
的直线交抛物线于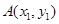 ,
,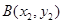
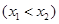 两点,且
两点,且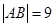 .
.(1)求该抛物线的方程;
(2)
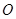 为坐标原点,是否存在平行于
为坐标原点,是否存在平行于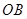 的直线
的直线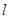 ,使得直线
,使得直线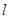 与抛物线有公共点,且
与抛物线有公共点,且 直线
直线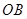 与
与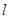 的距离为
的距离为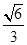 ?若存在,求出直线
?若存在,求出直线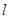 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.解:(1)设直线方程为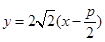 ,联立方程组
,联立方程组
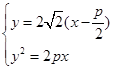
整理得到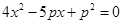 ,所以
,所以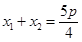 .
.
由抛物线定义得, ,所以
,所以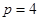 ,所以方程为
,所以方程为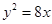 .……4分
.……4分
(2)可得 ,直线
,直线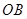 :
: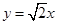
假设存在这样的直线,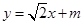 ,
,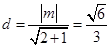 ,得
,得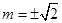 ……6分
……6分
经检验,直线方程为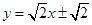 .……8分
.……8分
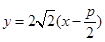 ,联立方程组
,联立方程组
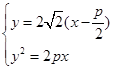
整理得到
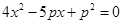 ,所以
,所以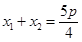 .
.由抛物线定义得,
 ,所以
,所以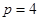 ,所以方程为
,所以方程为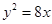 .……4分
.……4分(2)可得
 ,直线
,直线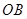 :
: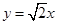
假设存在这样的直线,
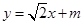 ,
,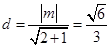 ,得
,得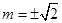 ……6分
……6分经检验,直线方程为
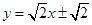 .……8分
.……8分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
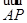 ·
·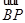 =k|
=k|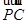 |2.
|2.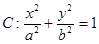 经过点(0,
经过点(0,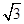 ),离心率为
),离心率为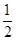 ,直线l经过椭圆C的右焦点F交
,直线l经过椭圆C的右焦点F交 椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.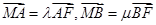 ,当直线l的倾斜角变化时,探求
,当直线l的倾斜角变化时,探求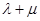 的值是否为定值?若是,求出
的值是否为定值?若是,求出
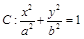
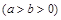 的离心率为
的离心率为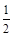 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线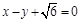 相切.
相切.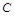 的方程;
的方程;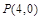 ,
,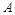 ,
,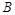 是椭圆
是椭圆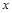 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结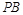 交椭圆
交椭圆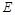 ,证明直线
,证明直线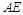 与
与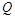 ;
;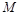 ,
,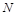 两点,求
两点,求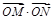 的取值范围.
的取值范围.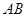 的两个端点
的两个端点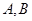 分别在
分别在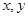 轴上移动,点
轴上移动,点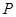 在直线
在直线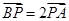 .(I)求点
.(I)求点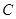 ,过点
,过点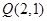 任作直线
任作直线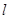 交曲线
交曲线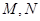 两点,过
两点,过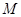 作斜率为
作斜率为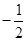 的直线
的直线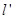 交曲线
交曲线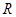 .求证:直线
.求证:直线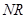 与直线
与直线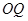 的交点为定点(
的交点为定点(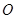 为坐标原点),并求出该定点.
为坐标原点),并求出该定点.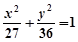 的焦点相同,且它们一个交点的纵坐标为4,则双曲线的虚轴长为
的焦点相同,且它们一个交点的纵坐标为4,则双曲线的虚轴长为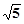
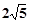
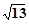
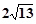
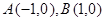 ,
,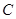 为平面内一动点,且满足
为平面内一动点,且满足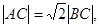 那么点
那么点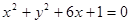
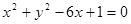
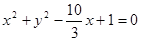

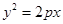 的准线与双曲线
的准线与双曲线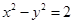 的左准线重合,则p的值为 ▲
的左准线重合,则p的值为 ▲ 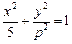 的左焦点在抛物线
的左焦点在抛物线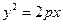 的准线上,则p的值为_______;
的准线上,则p的值为_______;