题目内容
9.已知$\overrightarrow{a}$、$\overrightarrow{b}$为平面向量,若$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$的夹角为$\frac{π}{4}$,$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,则$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$=( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 由向量加减的运算法则作图,用正弦定理解三角形可得.
解答 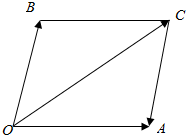 解:作向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,则$\overrightarrow{OC}$=$\overrightarrow{a}$+$\overrightarrow{b}$,
解:作向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,则$\overrightarrow{OC}$=$\overrightarrow{a}$+$\overrightarrow{b}$,
由平行四边形法则可得$\overrightarrow{AC}$=$\overrightarrow{b}$,
∵$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$的夹角为$\frac{π}{4}$,$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,
∴∠AOC=$\frac{π}{4}$,∠ACO=∠BOC=$\frac{π}{3}$,
在△OAC中由正弦定理可得$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$=$\frac{sin∠ACO}{sin∠AOC}$
=$\frac{sin\frac{π}{3}}{sin\frac{π}{4}}$=$\frac{\frac{\sqrt{3}}{2}}{\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{3}}{\sqrt{2}}$=$\frac{\sqrt{6}}{2}$,
故选:B.
点评 本题考查平面向量的夹角,涉及解三角形,数形结合是解决问题的关键,属中档题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
16.下列表示正确的是( )
| A. | 0∈∅ | B. | 3∈{偶数} | C. | 0∈{x|0<x<1} | D. | 1∈{|x2-1=0} |
17.若x,y∈[-$\frac{π}{2}$,$\frac{π}{2}$],且xsinx-ysiny>0,那么下面关系正确的是( )
| A. | x>y | B. | x+y>0 | C. | x<y | D. | x2>y2 |
1.f(x)=$\left\{\begin{array}{l}{x+2,}&{x≤-1}\\{{x}^{2},}&{-1<x<2}\\{2x,}&{x≥2}\end{array}\right.$,若f(x0)=3,则x0=( )
| A. | 3 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
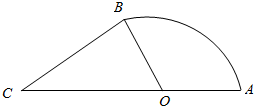 广告公司为某游乐场设计某项设施的宣传画,根据该设施的外观,设计成的平面图由半径为2m的扇形AOB和三角区域BCO构成,其中C,O,A在一条直线上,∠ACB=$\frac{π}{4}$,记该设施平面图的面积为S(x)m2,∠AOB=xrad,其中$\frac{π}{2}$<x<π.
广告公司为某游乐场设计某项设施的宣传画,根据该设施的外观,设计成的平面图由半径为2m的扇形AOB和三角区域BCO构成,其中C,O,A在一条直线上,∠ACB=$\frac{π}{4}$,记该设施平面图的面积为S(x)m2,∠AOB=xrad,其中$\frac{π}{2}$<x<π.