题目内容
【题目】设函数f(x)=8lnx+15x﹣x2 , 数列{an}满足an=f(n),n∈N+ , 数列{an}的前n项和Sn最大时,n=( )
A.15
B.16
C.17
D.18
【答案】B
【解析】解:函数f(x)=8lnx+15x﹣x2 , x>0 导数为f′(x)= ![]() +15﹣2x=
+15﹣2x= ![]()
= ![]() ,
,
当x>8时,f′(x)<0,f(x)递减;当0<x<8时,f′(x)>0,f(x)递增,
可得x=8处f(x)取得极大值,且为最大值,f(8)=8ln8+120﹣64>0,
由an=f(n),n∈N+ , 可得f(1)=15﹣1=14>0,
f(16)=8ln16+15×16﹣162=8ln16﹣16>0,
f(17)=8ln17+15×17﹣172=8ln17﹣34<0,
由单调性可得a1 , a2 , …,a16都大于0,a17<0,
则数列{an}的前n项和Sn最大时,n=16.
故选:B.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系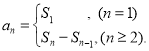 .
.

练习册系列答案
相关题目
