题目内容
【题目】[选修4-4：坐标系与参数方程选讲]
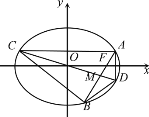
在直角坐标系xOy中，圆C的方程为（x﹣1）2+y2= 
，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，点M的极坐标为（2，θ），过点M斜率为1的直线交圆C于A，B两点．
（1）求圆C的极坐标方程；
（2）求|MA||MB|的范围．
【答案】
（1）解：∵圆C的方程为（x﹣1）2+y2= 
，即 
=0，
∴由x=ρcosθ，y=ρsinθ，得圆C的极坐标方程为： 
．
（2）解：∵点M的极坐标为（2，θ），∴点M的直角坐标为（2cosθ，2sinθ），
∴直线l的参数方程为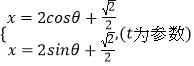 
，
直线l与圆C交于A，B两点，把直线参数方程代入圆C方程，得：
三，
，
解得0＜θ＜ 
， 
，
根据直线参数方程的几何意义得|MA||MB|=|t1t2|=| 
|，
∴|MA||MB|的取值范围是（ 
， 
）．
【解析】（1）由x=ρcosθ，y=ρsinθ，能求出圆C的极坐标方程．（2）点M的直角坐标为（2cosθ，2sinθ），从而直线l的参数方程为 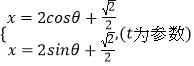，把直线参数方程代入圆C方程，得 ，由此利用根的判别式根据直线参数方程的几何意义能求出|MA||MB|的取值范围．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
