题目内容
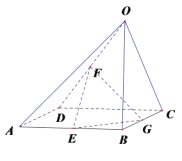
【题目】如图，四棱锥P-ABCD中，侧面PAD是边长为2的等边三角形且垂直于底
， 
是
的中点。
（1）证明：直线
平面
；
（2）点
在棱
上，且直线
与底面
所成角为
，求二面角
的余弦值。
【答案】（1）见解析；（2）
【解析】试题分析：（1） 取
的中点
，连结
， 
，由题意证得
∥
，利用线面平行的判断定理即可证得结论；（2）建立空间直角坐标系，求得半平面的法向量： 
， 
，然后利用空间向量的相关结论可求得二面角
的余弦值为
．
试题解析：（1）取
中点
，连结
， 
．
因为
为
的中点，所以
, 
,由
得
，又
所以
．四边形
为平行四边形， 
．
又
， 
，故
（2）
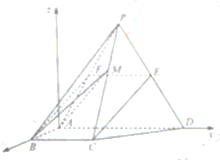
由已知得
,以A为坐标原点， 
的方向为x轴正方向， 
为单位长，建立如图所示的空间直角坐标系A-xyz,则
则
， 
， 
， 
，
,
则
因为BM与底面ABCD所成的角为45°，而
是底面ABCD的法向量，所以
， 
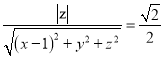
即（x-1）+y-z=0
又M在棱PC上，学|科网设
由①，②得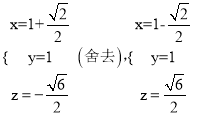
所以M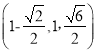
，从而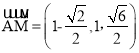
设
是平面ABM的法向量，则
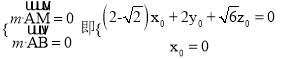
所以可取m=（0，-
，2）.于是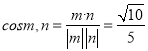
因此二面角M-AB-D的余弦值为
点睛:（1）求解本题要注意两点：①两平面的法向量的夹角不一定是所求的二面角，②利用方程思想进行向量运算，要认真细心、准确计算．
（2）设m，n分别为平面α，β的法向量，则二面角θ与<m，n>互补或相等，故有|cos θ|＝|cos<m，n>|=
．求解时一定要注意结合实际图形判断所求角是锐角还是钝角．
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
【题目】为及时了解适龄公务员对开放生育二胎政策的态度，某部门随机调查了90位30岁到40岁的公务员，得到情况如表：
（1）完成表格，并判断是否有99%以上的把握认为“生二胎意愿与性别有关”，并说明理由；
（2）现把以上频率当作概率，若从社会上随机独立抽取三位30岁到40岁的男公务员访问，求这三人中至少有一人有意愿生二胎的概率．
（3）已知15位有意愿生二胎的女性公务员中有两位来自省妇联，该部门打算从这15位有意愿生二胎的女性公务员中随机邀请两位来参加座谈，设邀请的2人中来自省女联的人数为X，求X的公布列及数学期望E（X）．
男性公务员 | 女性公务员 | 总计 | |
有意愿生二胎 | 30 | 15 | |
无意愿生二胎 | 20 | 25 | |
总计 |
附： 
P（k2≥k0） | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费
（单位：万元）对年销售量
（单位：吨）的影响，对近六年的年宣传费
和年销售量
(
)的数据作了初步统计，得到如下数据：
年份（ | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年宣传费 | 23 | 25 | 27 | 29 | 32 | 35 |
年销售量 | 11 | 21 | 24 | 66 | 115 | 325 |
（1）根据散点图判断
与
，哪一个更适合作为年销售量（吨）与关于宣传费（万元）的回归方程类型；
（2）规定当产品的年销售量（吨）与年宣传费（万元）的比值大于1时，认为该年效益良好，现从这6年中任选3年，记其中选到效益良好的数量为
，试求的所有取值情况及对应的概率；
（3）根据频率分布直方图中求出样本数据平均数的思想方法，求的平均数.
