题目内容
【题目】已知函数![]() ,若不等式
,若不等式![]() 在
在![]() 上恒成立,则实数
上恒成立,则实数![]() 的取值范围是( ).
的取值范围是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
将不等式变形后,构造函数g(x),结合选项对m讨论,利用导数分析函数的单调性及函数值的分布情况,对选项排除验证即可.
原不等式转化为![]() >0在
>0在![]() 上恒成立,
上恒成立,
记g(x)=![]() ,
,
由基本初等函数的图象及导数的几何意义可知,
y=x+1与y=x-1分别为y=![]() 与y=
与y=![]() 的切线,
的切线,
即![]() ,(x=0时等号成立),
,(x=0时等号成立),![]() (x=1时等号成立),可得
(x=1时等号成立),可得![]() (x=0时等号成立),
(x=0时等号成立),
∴m![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
又![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 在
在![]() 上恒成立,
上恒成立,
∴m![]() 时符合题意,排除A、B;
时符合题意,排除A、B;
当m>0时,验证C选项是否符合,只需代入m=3,此时g(x)=![]() ,
,
则![]() ,此时
,此时![]() 0,
0,
令![]() )在
)在![]() 上单调递增,且
上单调递增,且![]() ,∴
,∴![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上单调递增,而
上单调递增,而![]() 0,∴
0,∴![]() 在
在![]() 上恒成立,
上恒成立,
∴g(x)在![]() 上单调递增,又g(0)=0,∴g(x)
上单调递增,又g(0)=0,∴g(x)![]() 在
在![]() 上恒成立,
上恒成立,
即m=3符合题意,排除D,
故选C.

 名校课堂系列答案
名校课堂系列答案【题目】一般来说,一个人脚掌越长,他的身高就越高,现对10名成年人的脚掌![]() 与身高
与身高![]() 进行测量,得到数据(单位:cm)作为样本如表所示:
进行测量,得到数据(单位:cm)作为样本如表所示:
脚掌长( | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
身高( | 141 | 146 | 154 | 160 | 169 | 176 | 181 | 188 | 197 | 203 |
(1)在上表数据中,以“脚掌长”为横坐标,“身高”为纵坐标,作出散点图后,发现散点在一条直线附近,试求“身高”与“脚掌长”之间的线性回归方程![]() ;
;
(2)若某人的脚掌长为26.5cm,试估计此人的身高;
(3)在样本中,从身高180cm以上的4人中随机抽取2人进行进一步的分析,求所抽取的2人中至少有1人身高在190cm以上的概率.
(参考数据: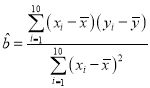 ,
, ,
,![]() ,
,![]() ,
,![]() )
)
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者![]() 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下![]() 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为![]() .
.
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
![]() 请完成上面的列联表;
请完成上面的列联表;
![]() 根据列联表的数据,能否有
根据列联表的数据,能否有![]() 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|