题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() 的准线被椭圆
的准线被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
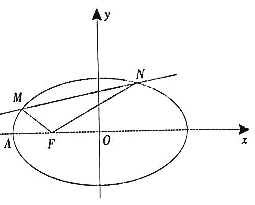
(2)如图,点![]() 分别是椭圆
分别是椭圆![]() 的左顶点、左焦点直线
的左顶点、左焦点直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() (
(![]() 都在
都在![]() 轴上方).且
轴上方).且![]() .证明:直线
.证明:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 过定点
过定点![]()
【解析】
(1)根据题意可得![]() 1,a2=2b2,求解即可.
1,a2=2b2,求解即可.
(2)设直线l的方程,代入椭圆方程,利用韦达定理及直线的斜率公式将条件转化,即可求k,m的关系式,代入直线方程即可求出定点.
(1)由题意可知,抛物线![]() 的准线方程为
的准线方程为![]() ,又椭圆
,又椭圆![]() 被准线截得弦长为
被准线截得弦长为![]() ,
,
∴点![]() 在椭圆上,∴
在椭圆上,∴![]() ,① 又
,① 又![]() ,∴
,∴![]() ,
,
∴![]() ,②,由①②联立,解得
,②,由①②联立,解得![]() ,∴椭圆
,∴椭圆![]() 的标准方程为:
的标准方程为:![]() ,
,
(2)设直线![]() ,设
,设![]() ,
,
把直线![]() 代入椭圆方程,整理可得
代入椭圆方程,整理可得![]() ,
,![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,∵
,∵![]() 都在
都在![]() 轴上方.且
轴上方.且![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
整理可得![]() ,∴
,∴![]() ,
,
即![]() ,整理可得
,整理可得![]() ,
,
∴直线![]() 为
为![]() ,∴直线
,∴直线![]() 过定点
过定点![]() .
.

练习册系列答案
相关题目
【题目】某校组织了一次新高考质量测评,在成绩统计分析中,某班的数学成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:
5 | 6 | 8 | ||||||||
6 | 2 | 3 | 3 | 5 | 6 | 8 | 9 | |||
7 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
8 | ||||||||||
9 | 5 | 8 |

(1)求该班数学成绩在![]() 的频率及全班人数;
的频率及全班人数;
(2)根据频率分布直方图估计该班这次测评的数学平均分;
(3)若规定90分及其以上为优秀,现从该班分数在80分及其以上的试卷中任取2份分析学生得分情况,求在抽取的2份试卷中至少有1份优秀的概率.

