题目内容
(本小题满分12分)
已知函数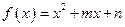 的图像过点
的图像过点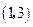 ,且
,且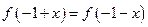 对任意实数都成
对任意实数都成
立,函数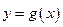 与
与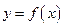 的图像关于原点对称.
的图像关于原点对称. 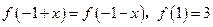 .
.
(Ⅰ)求 与
与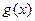 的解析式;
的解析式;
(Ⅱ)若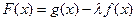 在[-1,1]上是增函数,求实数λ的取值范围.
在[-1,1]上是增函数,求实数λ的取值范围.
已知函数
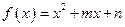 的图像过点
的图像过点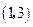 ,且
,且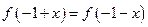 对任意实数都成
对任意实数都成立,函数
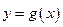 与
与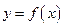 的图像关于原点对称.
的图像关于原点对称. 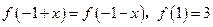 .
.(Ⅰ)求
 与
与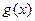 的解析式;
的解析式;(Ⅱ)若
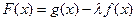 在[-1,1]上是增函数,求实数λ的取值范围.
在[-1,1]上是增函数,求实数λ的取值范围.解:⑴由题意知: ,
,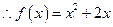
设函数 图象上的任意一点
图象上的任意一点 关于原点的对称点为P(x,y),
关于原点的对称点为P(x,y),
则 ,
,
因为点

⑵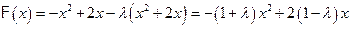
 连续,
连续,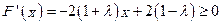 恒成立
恒成立
即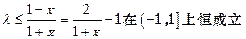 ,
,
由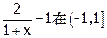 上为减函数,
上为减函数,
当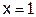 时取最小值0,
时取最小值0,
故
另解: ,
,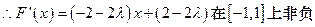
 ,解得
,解得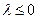
 ,
,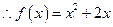
设函数
 图象上的任意一点
图象上的任意一点 关于原点的对称点为P(x,y),
关于原点的对称点为P(x,y), 则
 ,
, 因为点


⑵
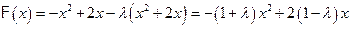
 连续,
连续,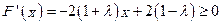 恒成立
恒成立即
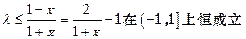 ,
,由
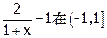 上为减函数,
上为减函数,当
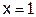 时取最小值0,
时取最小值0,故

另解:
 ,
,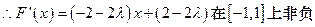
 ,解得
,解得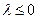
略

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
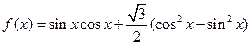 .
. 的值;
的值;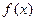 的最大值及单调递增区间.
的最大值及单调递增区间.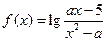 的定义域为
的定义域为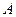 ,若命题
,若命题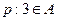 与命题
与命题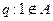 有且仅有一个为真命题,求实数
有且仅有一个为真命题,求实数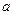 的取值范围。
的取值范围。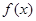 同时满足下列条件:①是奇函数;②在[0,1]上是增函数;③在
同时满足下列条件:①是奇函数;②在[0,1]上是增函数;③在 上的函数
上的函数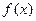 满足
满足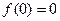 ,
,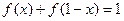 ,且
,且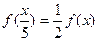 ,当
,当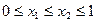 时,有
时,有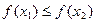 ,求
,求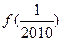 的值
的值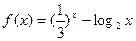 ,
,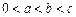 ,
,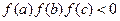 ,实数
,实数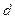 是函数
是函数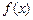 的一个零点.给出下列四个判断:
的一个零点.给出下列四个判断: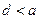 ;②
;②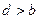 ;③
;③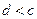 ;④
;④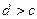 .
.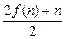 (n∈N*)且f(1)=2,则f(20)为( )
(n∈N*)且f(1)=2,则f(20)为( )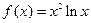 的单调递减区间为 .
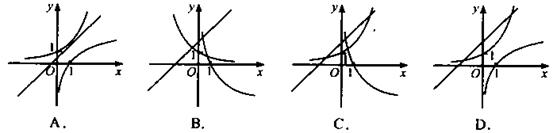
的单调递减区间为 .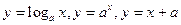 的图像,可能正确的是 ( )
的图像,可能正确的是 ( )