题目内容
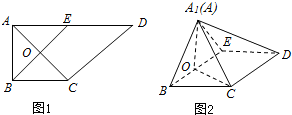
5.一种画椭圆的工具如图1所示.O是滑槽AB的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且DN=ON=1,MN=3,当栓子D在滑槽AB内作往复运动时,带动N绕O转动,M处的笔尖画出的椭圆记为C,以O为原点,AB所在的直线为x轴建立如图2所示的平面直角坐标系.(1)求椭圆C的方程;
(2)设动直线l与两定直线l1:x-2y=0和l2:x+2y=0分别交于P,Q两点.若直线l总与椭圆C有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
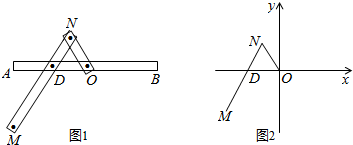
分析 (1)根据条件求出a,b即可求椭圆C的方程;
(2)联立直线方程和椭圆方程,求出原点到直线的距离,结合三角形的面积公式进行求解即可.
解答 解:(1)设D(t,0),|t|≤2,
N(x0,y0),M(x,y),由题意得$\overrightarrow{MD}$=2$\overrightarrow{DN}$,
且|$\overrightarrow{DN}$|=|$\overrightarrow{ON}$|=1,
∴(t-x,-y)=2(x0-t,y0),且$\left\{\begin{array}{l}{({x}_{0}-t)^{2}+{{y}_{0}}^{2}=1}\\{{{x}_{0}}^{2}+{{y}_{0}}^{2}=1}\end{array}\right.$,
即$\left\{\begin{array}{l}{t-x=2{x}_{0}-2t}\\{y=-2{y}_{0}}\end{array}\right.$,且t(t-2x0)=0,
由于当点D不动时,点N也不动,∴t不恒等于0,
于是t=2x0,故x0=$\frac{x}{4}$,y0=-$\frac{y}{2}$,
代入x02+y02=1,得方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1$.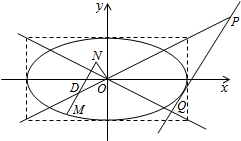
(2)①当直线l的斜率k不存在时,直线l为:x=4或x=-4,都有S△OPQ=$\frac{1}{2}×4×4=8$,
②直线l的斜率k存在时,直线l为:y=kx+m,(k$≠±\frac{1}{2}$),
由$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+4{y}^{2}=16}\end{array}\right.$消去y,可得(1+4k2)x2+8kmx+4m2-16=0,
∵直线l总与椭圆C有且只有一个公共点,
∴△=64k2m2-4(1+4k2)(4m2-16)=0,即m2=16k2+4,①,
由$\left\{\begin{array}{l}{y=kx+m}\\{x-2y=0}\end{array}\right.$,可得P($\frac{2m}{1-2k}$,$\frac{m}{1-2k}$),同理得Q($\frac{-2m}{1+2k}$,$\frac{m}{1+2k}$),
原点O到直线PQ的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$和|PQ|=$\sqrt{1+{k}^{2}}$•|xP-xQ|,
可得S△OPQ=$\frac{1}{2}$|PQ|d=$\frac{1}{2}$|m||xP-xQ|=$\frac{1}{2}$|m||$\frac{2m}{1-2k}+\frac{2m}{1+2k}$|=|$\frac{2{m}^{2}}{1-4{k}^{2}}$|②,
将①代入②得S△OPQ=|$\frac{2{m}^{2}}{1-4{k}^{2}}$|=8|$\frac{4{k}^{2}+1}{4{k}^{2}-1}$|,
当k2>$\frac{1}{4}$时,S△OPQ=8($\frac{4{k}^{2}+1}{4{k}^{2}-1}$)=8(1+$\frac{2}{4{k}^{2}-1}$)>8,
当0≤k2<$\frac{1}{4}$时,S△OPQ=8|$\frac{4{k}^{2}+1}{4{k}^{2}-1}$|=-8($\frac{4{k}^{2}+1}{4{k}^{2}-1}$)=8(-1+$\frac{2}{1-4{k}^{2}}$),
∵0≤k2<$\frac{1}{4}$时,∴0<1-4k2≤1,$\frac{2}{1-4{k}^{2}}$≥2,
∴S△OPQ=8(-1+$\frac{2}{1-4{k}^{2}}$)≥8,当且仅当k=0时取等号,
∴当k=0时,S△OPQ的最小值为8,
综上可知当直线l与椭圆C在四个顶点处相切时,三角形OPQ的面积存在最小值为8.
点评 本题主要考查椭圆方程的求解,以及直线和圆锥曲线的位置关系的应用,结合三角形的面积公式是解决本题的关键.综合性较强,运算量较大.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案| A. | $\frac{3}{4}$+$\frac{1}{2π}$ | B. | $\frac{1}{2}$+$\frac{1}{π}$ | C. | $\frac{1}{4}$-$\frac{1}{2π}$ | D. | $\frac{1}{2}$-$\frac{1}{π}$ |
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
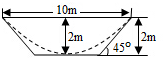 如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为1.2.
如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为1.2.