题目内容
13. 如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为1.2.
如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为1.2.
分析 建立直角坐标系,求出抛物线方程,然后利用定积分求出泥沙沉积的横截面面积,求出梯形面积,即可推出结果.
解答  解:如图:建立平面直角坐标系,设抛物线方程为:y=ax2,因为抛物线经过(5,2),可得a=$\frac{2}{25}$,
解:如图:建立平面直角坐标系,设抛物线方程为:y=ax2,因为抛物线经过(5,2),可得a=$\frac{2}{25}$,
所以抛物线方程:y=$\frac{2}{25}{x}^{2}$,
横截面为等腰梯形的水渠,泥沙沉积的横截面的面积为:
2×$({∫}_{0}^{5}\frac{2}{25}{x}^{2}-\frac{1}{2}×2×2)$=2($\frac{2}{75}{{x}^{3}|}_{0}^{5}-2$)=$\frac{8}{3}$,
等腰梯形的面积为:$\frac{10+6}{2}×2$=16,当前最大流量的横截面的面积16-$\frac{8}{3}$,
原始的最大流量与当前最大流量的比值为:$\frac{16}{16-\frac{8}{3}}$=1.2.
故答案为:1.2.
点评 本题考查抛物线的求法,定积分的应用,考查分析问题解决问题的能力,合理建系是解题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
2.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点为F,右顶点为A,过F作AF的垂线与双曲线交于B,C两点,过B,C分别作AC,AB的垂线,两垂线交于点D.若D到直线BC的距离小于a+$\sqrt{{a^2}+{b^2}}$,则该双曲线的渐近线斜率的取值范围是( )
| A. | (-1,0)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-$\sqrt{2}$,0)∪(0,$\sqrt{2}$) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
3.一辆小客车上有5名座位,其座号为1,2,3,4,5,乘客P1,P2,P3,P4,P5的座位号分别为1,2,3,4,5.他们按照座位号顺序先后上车,乘客P1因身体原因没有坐自己1号座位,这时司机要求余下的乘客按以下规则就坐:如果自己的座位空着,就只能坐自己的座位.如果自己的座位已有乘客就坐,就在这5个座位的剩余空位中选择座位.
(Ⅰ)若乘客P1坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
(Ⅱ)若乘客P1坐到了2号座位,其他乘客按规则就坐,求乘客P5坐到5号座位的概率.
(Ⅰ)若乘客P1坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
| 乘客 | P1 | P2 | P3 | P4 | P5 |
| 座位号 | 3 | 2 | 1 | 4 | 5 |
| 3 | 2 | 4 | 5 | 1 | |
| 3 | 2 | 4 | 1 | 5 | |
| 3 | 2 | 5 | 4 | 1 |
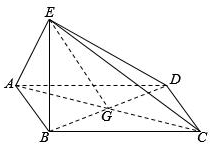 如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.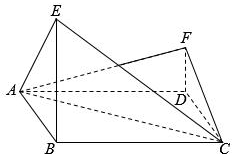 如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC.
如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC.