题目内容
17.“x>1”是“$lo{g_{\frac{1}{2}}}$(x+2)<0”的( )| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
分析 解“$lo{g_{\frac{1}{2}}}$(x+2)<0”,求出其充要条件,再和x>1比较,从而求出答案.
解答 解:由“$lo{g_{\frac{1}{2}}}$(x+2)<0”
得:x+2>1,解得:x>-1,
故“x>1”是“$lo{g_{\frac{1}{2}}}$(x+2)<0”的充分不必要条件,
故选:B.
点评 本题考察了充分必要条件,考察对数函数的性质,是一道基础题.

练习册系列答案
相关题目
7.已知实数变量x,y满足$\left\{\begin{array}{l}{x+y≥1}\\{x-y≥0}\\{2x-y-2≤0}\end{array}\right.$,则z=3x-y的最大值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点为F,右顶点为A,过F作AF的垂线与双曲线交于B,C两点,过B,C分别作AC,AB的垂线,两垂线交于点D.若D到直线BC的距离小于a+$\sqrt{{a^2}+{b^2}}$,则该双曲线的渐近线斜率的取值范围是( )
| A. | (-1,0)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-$\sqrt{2}$,0)∪(0,$\sqrt{2}$) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
7.某几何体的三视图如图所示,则该几何体的表面积等于( )
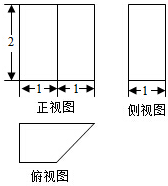

| A. | 8+2$\sqrt{2}$ | B. | 11+2$\sqrt{2}$ | C. | 14+2$\sqrt{2}$ | D. | 15 |
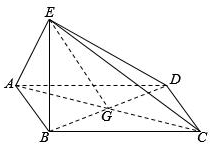 如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.