题目内容
20.已知函数f(x)=x3+ax+$\frac{1}{4}$,g(x)=-lnx(i)当 a为何值时,x轴为曲线y=f(x)的切线;
(ii)用min {m,n }表示m,n中的最小值,设函数h(x)=min { f(x),g(x)}(x>0),讨论h(x)零点的个数.
分析 (i)f′(x)=3x2+a.设曲线y=f(x)与x轴相切于点P(x0,0),则f(x0)=0,f′(x0)=0解出即可.
(ii)对x分类讨论:当x∈(1,+∞)时,g(x)=-lnx<0,可得函数h(x)=min { f(x),g(x)}≤g(x)<0,即可得出零点的个数.
当x=1时,对a分类讨论:a≥-$\frac{5}{4}$,a<-$\frac{5}{4}$,即可得出零点的个数;
当x∈(0,1)时,g(x)=-lnx>0,因此只考虑f(x)在(0,1)内的零点个数即可.对a分类讨论:①当a≤-3或a≥0时,②当-3<a<0时,利用导数研究其单调性极值即可得出.
解答 解:(i)f′(x)=3x2+a.
设曲线y=f(x)与x轴相切于点P(x0,0),则f(x0)=0,f′(x0)=0,
∴$\left\{\begin{array}{l}{{x}_{0}^{3}+a{x}_{0}+\frac{1}{4}=0}\\{3{x}_{0}^{2}+a=0}\end{array}\right.$,解得${x}_{0}=\frac{1}{2}$,a=$-\frac{3}{4}$.
因此当a=-$\frac{3}{4}$时,x轴为曲线y=f(x)的切线;
(ii)当x∈(1,+∞)时,g(x)=-lnx<0,
∴函数h(x)=min { f(x),g(x)}<0,
故h(x)在x∈(1,+∞)时无零点.
当x=1时,若a≥-$\frac{5}{4}$,则f(1)=a+$\frac{5}{4}$≥0,
∴h(x)=min { f(1),g(1)}=g(1)=0,故x=1是函数h(x)的一个零点;
若a<-$\frac{5}{4}$,则f(1)=a+$\frac{5}{4}$<0,∴h(x)=min { f(1),g(1)}=f(1)<0,故x=1不是函数h(x)的零点;
当x∈(0,1)时,g(x)=-lnx>0,因此只考虑f(x)在(0,1)内的零点个数即可.
①当a≤-3或a≥0时,f′(x)=3x2+a在(0,1)内无零点,因此f(x)在区间(0,1)内单调,
而f(0)=$\frac{1}{4}$,f(1)=a+$\frac{5}{4}$,∴当a≤-3时,函数f(x)在区间(0,1)内有一个零点,
当a≥0时,函数f(x)在区间(0,1)内没有零点.
②当-3<a<0时,函数f(x)在$(0,\sqrt{\frac{-a}{3}})$内单调递减,在$(\sqrt{\frac{-a}{3}},1)$内单调递增,故当x=$\sqrt{\frac{-a}{3}}$时,f(x)取得最小值$f(\sqrt{\frac{-a}{3}})$=$\frac{2a}{3}\sqrt{\frac{-a}{3}}+\frac{1}{4}$.
若$f(\sqrt{\frac{-a}{3}})$>0,即$-\frac{3}{4}<a<0$,则f(x)在(0,1)内无零点.
若$f(\sqrt{\frac{-a}{3}})$=0,即a=-$\frac{3}{4}$,则f(x)在(0,1)内有唯一零点.
若$f(\sqrt{\frac{-a}{3}})$<0,即$-3<a<-\frac{3}{4}$,由f(0)=$\frac{1}{4}$,f(1)=a+$\frac{5}{4}$,
∴当$-\frac{5}{4}<a<-\frac{3}{4}$时,f(x)在(0,1)内有两个零点.当-3<a$≤-\frac{5}{4}$时,f(x)在(0,1)内有一个零点.
综上可得:a<$-\frac{5}{4}$时,函数h(x)有一个零点.
当$a>-\frac{3}{4}$时,h(x)有一个零点;
当a=$-\frac{3}{4}$或$-\frac{5}{4}$时,h(x)有两个零点;
当$-\frac{5}{4}<a<-\frac{3}{4}$时,函数h(x)有三个零点.
点评 本题考查了导数的运算法则、利用导数的几何意义研究切线方程、利用导数研究函数的单调性极值,考查了分类讨论思想方法、推理能力与计算能力,属于难题.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案| A. | 0.648 | B. | 0.432 | C. | 0.36 | D. | 0.312 |
| A. | 既是奇函数又是减函数 | B. | 既是奇函数又是增函数 | ||
| C. | 是有零点的减函数 | D. | 是没有零点的奇函数 |
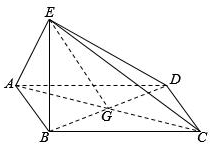 如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.