题目内容
13.设复数z=(x-1)+yi(x,y∈R),若|z|≤1,则y≥x的概率为( )| A. | $\frac{3}{4}$+$\frac{1}{2π}$ | B. | $\frac{1}{2}$+$\frac{1}{π}$ | C. | $\frac{1}{4}$-$\frac{1}{2π}$ | D. | $\frac{1}{2}$-$\frac{1}{π}$ |
分析 判断复数对应点图形,利用几何概型求解即可.
解答 解:复数z=(x-1)+yi(x,y∈R),若|z|≤1,它的几何意义是以(1,0)为圆心,1为半径的圆以及内部部分.y≥x的图形是图形中阴影部分,如图: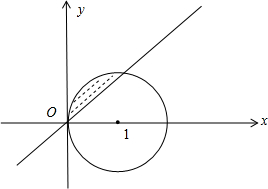
复数z=(x-1)+yi(x,y∈R),若|z|≤1,则y≥x的概率:$\frac{\frac{1}{4}π-\frac{1}{2}×1×1}{π}$=$\frac{1}{4}-\frac{1}{2π}$.
故选:C.
点评 本题考查复数的几何意义,几何概型的求法,考查计算能力以及数形结合的能力.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
4. 如图,在圆O中,M、N是弦AB的三等分点,弦CD,CE分别经过点M,N,若CM=2,MD=4,CN=3,则线段NE的长为( )
如图,在圆O中,M、N是弦AB的三等分点,弦CD,CE分别经过点M,N,若CM=2,MD=4,CN=3,则线段NE的长为( )
 如图,在圆O中,M、N是弦AB的三等分点,弦CD,CE分别经过点M,N,若CM=2,MD=4,CN=3,则线段NE的长为( )
如图,在圆O中,M、N是弦AB的三等分点,弦CD,CE分别经过点M,N,若CM=2,MD=4,CN=3,则线段NE的长为( )| A. | $\frac{8}{3}$ | B. | 3 | C. | $\frac{10}{3}$ | D. | $\frac{5}{2}$ |
