题目内容
16.设 a为实数,函数 f(x)=(x-a)2+|x-a|-a(a-1).(1)若f(0)≤1,求a的取值范围;
(2)讨论 f(x)的单调性;
(3)当a≥2 时,讨论f(x)+$\frac{4}{x}$ 在区间 (0,+∞)内的零点个数.
分析 (1)利用f(0)≤1,得到|a|+a-1≤0,对a分类讨论求解不等式的解集即可.
(2)化简函数f(x)的解析式,通过当x<a时,当x≥a时,利用二次函数f(x)的对称轴求解函数的单调区间即可.
(3)化简F(x)=f(x)+$\frac{4}{x}$,求出函数的导数,利用导函数的符号,通过a的讨论判断函数的单调性,然后讨论函数的零点的个数.
解答 解:(1)若f(0)≤1,即:a2+|a|-a(a-1)≤1.可得|a|+a-1≤0,
当a≥0时,a$≤\frac{1}{2}$,可得a∈[0,$\frac{1}{2}$].
当a<0时,|a|+a-1≤0,恒成立.
综上a$≤\frac{1}{2}$.
∴a的取值范围:$(-∞,\frac{1}{2}]$;
(2)函数 f(x)=$\left\{\begin{array}{l}{x}^{2}-(2a+1)x+2a,x<a\\{x}^{2}+(1-2a)x,x≥a\end{array}\right.$=$\left\{\begin{array}{l}{[x-(a+\frac{1}{2})]}^{2}-\frac{(2a-1)^{2}}{4},x<a\\{[x-(a-\frac{1}{2})]}^{2}-\frac{(2a-1)^{2}}{4},x≥a\end{array}\right.$,
当x<a时,函数f(x)的对称轴为:x=$\frac{2a+1}{2}$=a+$\frac{1}{2}$>a,
y=f(x)在(-∞,a)时是减函数,
当x≥a时,函数f(x)的对称轴为:x=$\frac{2a-1}{2}$=a-$\frac{1}{2}$<a,
y=f(x)在(a,+∞)时是增函数,
(3)F(x)=f(x)+$\frac{4}{x}$=$\left\{\begin{array}{l}{x}^{2}-(2a+1)x+\frac{4}{x}+2a,x<a\\{x}^{2}+(1-2a)x+\frac{4}{x},x≥a\end{array}\right.$,
$F′(x)=\left\{\begin{array}{l}2x-(2a+1)-\frac{4}{{x}^{2}}=\frac{2{x}^{3}-(2a+1){x}^{2}-4}{{x}^{2}},x<a\\ 2x+(1-2a)-\frac{4}{{x}^{2}}=\frac{2{x}^{3}+(1-2a){x}^{2}-4}{{x}^{2}},x≥a\end{array}\right.$,
当x<a时,$F′(x)=\frac{2{x}^{3}-(2a+1){x}^{2}-4}{{x}^{2}}$=$\frac{2{x}^{2}(x-a)-({x}^{2}+4)}{{x}^{2}}<0$,
所以,函数F(x)在(0,a)上是减函数.
当x≥a时,因为a≥2,所以,F′(x)=$\frac{2{x}^{3}+(1-2a){x}^{2}-4}{{x}^{2}}$═$\frac{2{x}^{2}(x-a)+({x}^{2}-4)}{{x}^{2}}≥0$,
所以,函数F(x)在(a,+∞)上是增函数.
F(a)=a-a2+$\frac{4}{a}$.当a=2时,F(2)=0,此时F(x)有一个零点,当a>2时,F(a)=a-a2+$\frac{4}{a}$,
F′(a)=1-2a$-\frac{4}{{a}^{2}}$=$\frac{-2{a}^{3}+{a}^{2}-4}{{a}^{2}}$=$\frac{{a}^{2}(1-a)-({a}^{3}+4)}{{a}^{2}}<0$.
所以F(ah)在(2,+∞)上是减函数,
所以F(a)<$F(2)=2-{2}^{2}+\frac{4}{2}=0$,即F(a)<0,
当x>0且x→0时,F(x)→+∞;当x→+∞时,F(x)→+∞,所以函数F(x)有两个零点.
综上所述,当a=2时,F(x)有一个零点,a>2时F(x)有两个零点.
点评 本题考查的知识点比较多,包括绝对值不等式的解法,函数的零点,函数的导数以及导数与函数的单调性的关系,考查分类讨论思想的应用,函数与方程的思想,转化思想的应用,也考查化归思想的应用.

 阅读快车系列答案
阅读快车系列答案 如图,在圆O中,M、N是弦AB的三等分点,弦CD,CE分别经过点M,N,若CM=2,MD=4,CN=3,则线段NE的长为( )
如图,在圆O中,M、N是弦AB的三等分点,弦CD,CE分别经过点M,N,若CM=2,MD=4,CN=3,则线段NE的长为( )| A. | $\frac{8}{3}$ | B. | 3 | C. | $\frac{10}{3}$ | D. | $\frac{5}{2}$ |
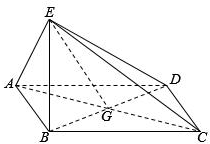 如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.