��Ŀ����
10����֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������ΪF��-c��0����������Ϊ$\frac{{\sqrt{3}}}{3}$����M����Բ����λ�ڵ�һ���ޣ�ֱ��FM��Բx2+y2=$\frac{b^2}{4}$�صõ��߶εij�Ϊc��|FM|=$\frac{{4\sqrt{3}}}{3}$��������ֱ��FM��б�ʣ�
��������Բ�ķ��̣�
�����趯��P����Բ�ϣ���ֱ��FP��б�ʴ���$\sqrt{2}$����ֱ��OP��OΪԭ�㣩��б�ʵ�ȡֵ��Χ��
���� ����ͨ��������Ϊ$\frac{{\sqrt{3}}}{3}$������ɵ�a2=3c2��b2=2c2����ֱ��FM�ķ���Ϊy=k��x+c�������ù��ɶ��������ľʽ������ɵý��ۣ�
����ͨ��������Բ��ֱ��FM�ķ��̣��ɵ�M��c��$\frac{2\sqrt{3}}{3}$c��������|FM|=$\frac{{4\sqrt{3}}}{3}$���㼴�ɣ�
�����趯��P������Ϊ��x��y�����ֱ�����ֱ��FP��ֱ��OP����Բ���̣���x�ʣ�-$\frac{3}{2}$��-1����x�ʣ�-1��0������������ۼ��ɵõ����ۣ�
��� �⣺����������Ϊ$\frac{{\sqrt{3}}}{3}$����$\frac{{c}^{2}}{{a}^{2}}$=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}$=$\frac{1}{3}$��
��2a2=3b2����a2=3c2��b2=2c2��
��ֱ��FM��б��Ϊk��k��0������ֱ��FM�ķ���Ϊy=k��x+c����
��ֱ��FM��Բx2+y2=$\frac{b^2}{4}$�صõ��߶εij�Ϊc��
��Բ�ģ�0��0����ֱ��FM�ľ���d=$\frac{|kc|}{\sqrt{1+{k}^{2}}}$��
��d2+$��\frac{c}{2}��^{2}$=$��\frac{b}{2}��^{2}$������$\frac{|kc|}{\sqrt{1+{k}^{2}}}$��2+$��\frac{c}{2}��^{2}$=$��\frac{b}{2}��^{2}$��
���k=$\frac{\sqrt{3}}{3}$����ֱ��FM��б��Ϊ$\frac{\sqrt{3}}{3}$��
�����ɣ�I������Բ����Ϊ��$\frac{{x}^{2}}{3{c}^{2}}$+$\frac{{y}^{2}}{2{c}^{2}}$=1��ֱ��FM�ķ���Ϊy=$\frac{\sqrt{3}}{3}$��x+c����
�����������̣���ȥy��������3x2+2cx-5c2=0�����x=-$\frac{5}{3}$c����x=c��
�ߵ�M�ڵ�һ���ޣ���M��c��$\frac{2\sqrt{3}}{3}$c����
��|FM|=$\frac{{4\sqrt{3}}}{3}$����$\sqrt{��c+c��^{2}+��\frac{2\sqrt{3}}{3}c-0��^{2}}$=$\frac{{4\sqrt{3}}}{3}$��
���c=1����a2=3c2=3��b2=2c2=2��
����Բ�ķ���Ϊ$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1��
�����趯��P������Ϊ��x��y����ֱ��FP��б��Ϊt��
��F��-1��0������t=$\frac{y-0}{x+1}$����y=t��x+1����x��-1����
����������$\left\{\begin{array}{l}{y=t��x+1��}\\{\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1}\end{array}\right.$����ȥy����������2x2+3t2��x+1��2=6��
�֡�ֱ��FP��б�ʴ���$\sqrt{2}$��
��$\sqrt{\frac{6-2{x}^{2}}{3��x+1��^{2}}}$��$\sqrt{2}$��6-2x2��6��x+1��2��
�����ã�x��2x+3����0��x��-1��
���-$\frac{3}{2}$��x��-1����-1��x��0��
��ֱ��OP��б��Ϊm����m=$\frac{y}{x}$����y=mx��x��0����
����������$\left\{\begin{array}{l}{y=mx}\\{\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1}\end{array}\right.$����ȥy����������m2=$\frac{2}{{x}^{2}}$-$\frac{2}{3}$��
�ٵ�x�ʣ�-$\frac{3}{2}$��-1��ʱ����y=t��x+1����0�����m��0��
��m=$\sqrt{\frac{2}{{x}^{2}}-\frac{2}{3}}$����m�ʣ�$\frac{\sqrt{2}}{3}$��$\frac{2\sqrt{3}}{3}$����
�ڵ�x�ʣ�-1��0��ʱ����y=t��x+1����0�����m��0��
��m=-$\sqrt{\frac{2}{{x}^{2}}-\frac{2}{3}}$����m�ʣ�-�ޣ�-$\frac{2\sqrt{3}}{3}$����
����������ֱ��OP��б�ʵ�ȡֵ��Χ�ǣ���-�ޣ�-$\frac{2\sqrt{3}}{3}$���ȣ�$\frac{\sqrt{2}}{3}$��$\frac{2\sqrt{3}}{3}$����
���� ���⿼����Բ�ı����̺ͼ������ʡ�ֱ�߷��̺�Բ�ķ��̡�ֱ����Բ��λ�ù�ϵ��һԪ���β���ʽ�Ȼ���֪ʶ�������ô��������о�Բ���ߵ����ʣ�������������������Լ��ú����뷽��˼��������������������е��⣮

| A�� | A=B | B�� | A��B=∅ | C�� | A$\stackrel{?}{��}$B | D�� | B$\stackrel{?}{��}$A |
| A�� | ��-1��0���ȣ�0��1�� | B�� | ��-�ޣ�-1���ȣ�1��+�ޣ� | C�� | ��-$\sqrt{2}$��0���ȣ�0��$\sqrt{2}$�� | D�� | ��-�ޣ�-$\sqrt{2}$���ȣ�$\sqrt{2}$��+�ޣ� |
| A�� | $\frac{1}{7}$ | B�� | $\frac{1}{6}$ | C�� | $\frac{5}{7}$ | D�� | $\frac{5}{6}$ |
| A�� | {0} | B�� | {1} | C�� | {0��1��2} | D�� | {0��1} |
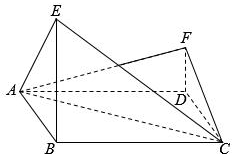 ��ͼ���ı���ABCDΪ���Σ���ABC=120�㣬E��F��ƽ��ABCDͬһ������㣬BE�Aƽ��ABCD��DF�Aƽ�� ABCD��BE=2DF��AE�AEC��
��ͼ���ı���ABCDΪ���Σ���ABC=120�㣬E��F��ƽ��ABCDͬһ������㣬BE�Aƽ��ABCD��DF�Aƽ�� ABCD��BE=2DF��AE�AEC��