Question

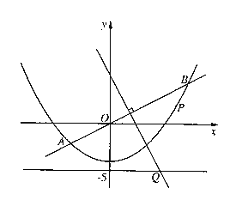
【题目】在平面直角坐标系中，已知点，的坐标分别为，．直线，相交于点，且它们的斜率之积是．记点的轨迹为．

（Ⅰ）求的方程．

（Ⅱ）已知直线，分别交直线于点，，轨迹在点处的切线与线段交于点，求的值．

Answer 1

【答案】（1）（2）1

【解析】

试题分析：（I）设出坐标为，求出直线的斜率和直线的斜率，利用斜率成绩为，整理即可得出曲线的方程；（II）设出坐标，得出，的方程，进一步求出点的纵坐标，写出椭圆在的切线方程，由判别式等于得到过的斜率（用的坐标表示），代入切线方程，求得点的纵坐标，设，转化为坐标关键，即可求出，得出的值．

试题解析：解法一：（Ⅰ）设点坐标为，则直线的斜率（）；直线的斜率（）．

由已知有（），

化简得点的轨迹的方程为（）．

（Ⅱ）设（），则．

直线的方程为，令，得点纵坐标为；

直线的方程为，令，得点纵坐标为；

设在点处的切线方程为，

由得．

由，得，

整理得．

将代入上式并整理得，解得，

所以切线方程为．

令得，点纵坐标为．

设，所以，所以

所以．

将代入上式，，解得，即．

解法二：（Ⅰ）同解法一．

（Ⅱ）设（），则．

直线的方程为，令，得点纵坐标为；

直线的方程为，令，得点纵坐标为；

设在点处的切线方程为，

由得．

由，得，

整理得．

将代入上式并整理得，解得，

所以切线方程为．

令得，点纵坐标为．

所以，

所以为线段的中点，即．