Question

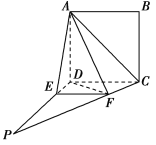
【题目】如图，四边形ABCD为正方形，PD⊥平面ABCD，∠DPC＝30°，AF⊥PC于点F，FE∥CD，交PD于点E.

(1)证明：CF⊥平面ADF；

(2)求二面角DAFE的余弦值．

Answer 1

【答案】（1）见解析（2）

【解析】

（1）结合已知又直线和平面垂直的判定定理可判F，即得所求；
（2）由已知数据求出必要的线段的长度，建立空间直角坐标系，由向量法计算即可．

(1)证明：∵PD⊥平面ABCD，AD平面ABCD，

∴PD⊥AD．

又CD⊥AD，PD∩CD＝D，∴AD⊥平面PCD．

又PC平面PCD，∴AD⊥PC．

又AF⊥PC，AD∩AF＝A，∴PC⊥平面ADF，即CF⊥平面ADF.

(2)设AB＝1，则在Rt△PCD中，CD＝1，

又∠DPC＝30°，∴PC＝2，PD＝，∠PCD＝60°.

由(1)知CF⊥DF，∴DF＝CDsin 60°＝，CF＝CDcos 60°＝.

又FE∥CD，∴＝＝，∴DE＝.

同理EF＝CD＝.

如图所示，以D为原点，建立空间直角坐标系Dxyz，

则A(0,0,1)，E，F，P(，0,0)，C(0,1,0)．

设m＝(x，y，z)是平面AEF的一个法向量，则

又＝，＝，∴

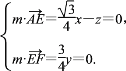
令x＝4，则z＝，m＝(4,0，)．由(1)知平面ADF的一个法向量为＝(－，1,0)，

设二面角 DAFE的平面角为θ，可知θ为锐角，

故cos θ＝|cos〈m，〉|＝＝＝.

故二面角DAFE的余弦值为.