题目内容
【题目】如图,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(I)见解析(II)![]() (III)
(III)![]()
【解析】试题
(Ⅰ)取![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,由题意可得平面
轴建立空间直角坐标系,由题意可得平面![]() 的法向量
的法向量![]() ,且
,且![]() ,据此有
,据此有![]() ,则
,则![]() 平面
平面![]() .
.
(Ⅱ)由题意可得平面![]() 的法向量
的法向量![]() ,结合(Ⅰ)的结论可得
,结合(Ⅰ)的结论可得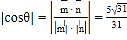 ,即平面
,即平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.
(Ⅲ)设![]() ,
,![]() ,则
,则![]() ,而平面
,而平面![]() 的法向量
的法向量![]() ,据此可得
,据此可得![]() ,解方程有
,解方程有![]() 或
或![]() .据此计算可得
.据此计算可得![]() .
.
试题解析:
(Ⅰ)取![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
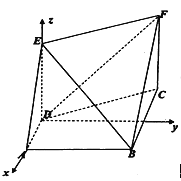
所在直线为![]() 轴建立空间直角坐标系,如图,则
轴建立空间直角坐标系,如图,则![]() ,
,![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,∴
,∴![]() 不妨设
不妨设![]() ,又
,又![]() ,
,
∴![]() ,∴
,∴![]() ,又∵
,又∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)∵![]() ,
,![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,
,
∴![]() 不妨设
不妨设![]() ,∴
,∴ ,
,
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.
(Ⅲ)设![]()
![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,又∵平面
,又∵平面![]() 的法向量
的法向量![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() 或
或![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() ;当
;当![]() 时,
时,![]() ,∴
,∴![]() .
.
综上,![]() .
.

【题目】某校在学年期末举行“我最喜欢的文化课”评选活动,投票规则是一人一票,高一(1)班44名学生和高一(7)班45名学生的投票结果如下表(无废票):
语文 | 数学 | 外语 | 物理 | 化学 | 生物 | 政治 | 历史 | 地理 | |
高一(1)班 | 6 | 9 | 7 | 5 | 4 | 5 | 3 | 3 | 2 |
高一(7)班 |
| 6 |
| 4 | 5 | 6 | 5 | 2 | 3 |
该校把上表的数据作为样本,把两个班同一学科的得票之和定义为该年级该学科的“好感指数”.
(Ⅰ)如果数学学科的“好感指数”比高一年级其他文化课都高,求![]() 的所有取值;
的所有取值;
(Ⅱ)从高一(1)班投票给政治、历史、地理的学生中任意选取![]() 位同学,设随机变量
位同学,设随机变量![]() 为投票给地理学科的人数,求
为投票给地理学科的人数,求![]() 的分布列和期望;
的分布列和期望;
(Ⅲ)当![]() 为何值时,高一年级的语文、数学、外语三科的“好感指数”的方差最小?(结论不要求证明)
为何值时,高一年级的语文、数学、外语三科的“好感指数”的方差最小?(结论不要求证明)
【题目】某企业对现有设备进行了改造,为了了解设备改造后的效果,现从设备改造前后生产的大量产品中各抽取了100件产品作为样本,检测其质量指标值,若质量指标值在![]() 内,则该产品视为合格品,否则视为不合格品.图1是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
内,则该产品视为合格品,否则视为不合格品.图1是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.

(1)完成![]() 列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关:
列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关:
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(2)根据图1和表1提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)企业将不合格品全部销毁后,根据客户需求对合格品进行等级细分,质量指标值落在![]() 内的定为一等品,每件售价180元;质量指标值落在
内的定为一等品,每件售价180元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件售价150元;其他的合格品定为三等品,每件售价120元.根据频数分布表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有合格产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
内的定为二等品,每件售价150元;其他的合格品定为三等品,每件售价120元.根据频数分布表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有合格产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
【题目】某制造商3月生产了一批乒乓球,从中随机抽样100个进行检查,测得每个球的直径(单位:mm),将数据分组如下:
分组 | 频数 | 频率 |
[39.95,39.97) | 10 | |
[39. 97,39.99) | 20 | |
[39.99,40.01) | 50 | |
[40.01,40.03] | 20 | |
合计 | 100 |

(Ⅰ)请在上表中补充完成频率分布表(结果保留两位小数),并在图中画出频率分布直方图;
(Ⅱ)若以上述频率作为概率,已知标准乒乓球的直径为40.00 mm,试求这批球的直径误差不超过0.03 mm的概率;
(Ⅲ)统计方法中,同一组数据经常用该组区间的中点值(例如区间[39.99,40.01)的中点值是40.00作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).


