题目内容
(x+
)5(x∈i且x≠0)展开式中x3的系数为10,则实数a等于 .
| a |
| x |
考点:二项式系数的性质
专题:二项式定理
分析:先求出二项式展开式的通项公式,再令x的幂指数等于3,求得r的值,即可求得展开式中x3的系数的值,再根据x3的系数为10,求得a的值.
解答:
解:(x+
)5(x∈i且x≠0)展开式的通项公式为Tr+1=
•ar•x5-2r,令5-2r=3,求得r=1,
可得展开式中x3的系数为
•a=10,求得a=2,
故答案为:2.
| a |
| x |
| C | r 5 |
可得展开式中x3的系数为
| C | 1 5 |
故答案为:2.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
设a,b,c,d∈R,给出下列命题:
①若ac>bc,则a>b;
②若a>b,c>d,则a+c>b+d;
③若a>b,c>d,则ac>bd;
④若ac2>bc2,则a>b.
其中真命题的序号是( )
①若ac>bc,则a>b;
②若a>b,c>d,则a+c>b+d;
③若a>b,c>d,则ac>bd;
④若ac2>bc2,则a>b.
其中真命题的序号是( )
| A、①② | B、②④ |
| C、①②④ | D、②③④ |
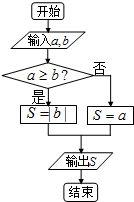 定义某种运算⊕,a⊕b的运算原理如图所示,设S=1⊕x,x∈[-2,2],则输出的S的最大值与最小值的差为( )
定义某种运算⊕,a⊕b的运算原理如图所示,设S=1⊕x,x∈[-2,2],则输出的S的最大值与最小值的差为( )| A、2 | B、-1 | C、4 | D、3 |
函数y=x2-1的值域是( )
| A、[-1,+∞) |
| B、R |
| C、[0,+∞) |
| D、[1,+∞) |
直线y=2x+1与y轴的交点所组成的集合为( )
| A、{0,1} | ||
| B、{(0,1)} | ||
C、{-
| ||
D、{(-
|
有一半径为4的圆,现将一枚直径为2的硬币投向其中(硬币与圆面有公共点就算是有效试验,硬币完全落在圆外的不计),则硬币完全落入圆内的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
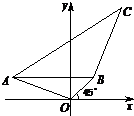 如图,在平面直角坐标系xOy中,已知点A(-3,1),直线OB的倾斜角为45°,且|OB|=
如图,在平面直角坐标系xOy中,已知点A(-3,1),直线OB的倾斜角为45°,且|OB|=