题目内容
设a，b，c，d∈R，给出下列命题：
①若ac＞bc，则a＞b；
②若a＞b，c＞d，则a+c＞b+d；
③若a＞b，c＞d，则ac＞bd；
④若ac2＞bc2，则a＞b．
其中真命题的序号是（ ）
①若ac＞bc，则a＞b；
②若a＞b，c＞d，则a+c＞b+d；
③若a＞b，c＞d，则ac＞bd；
④若ac2＞bc2，则a＞b．
其中真命题的序号是（ ）
| A、①② | B、②④ |
| C、①②④ | D、②③④ |
考点：不等式的基本性质
专题：不等式的解法及应用
分析：①若ac＞bc，则a＞b，c≤0时不成立；
②利用不等式的基本性质即可得出；
③若a＞b，c＞d，取a=2，b=1，c=-2，d=-3，则ac＜bd，即可判断出；
④若ac2＞bc2，则c2＞0，可得a＞b．
②利用不等式的基本性质即可得出；
③若a＞b，c＞d，取a=2，b=1，c=-2，d=-3，则ac＜bd，即可判断出；
④若ac2＞bc2，则c2＞0，可得a＞b．
解答：
解：①若ac＞bc，则a＞b，c≤0时不成立；
②若a＞b，c＞d，则a+c＞b+d，正确；
③若a＞b，c＞d，取a=2，b=1，c=-2，d=-3，则ac＜bd，不成立；
④若ac2＞bc2，则a＞b，正确．
其中真命题的序号是②④．
故选：B．
②若a＞b，c＞d，则a+c＞b+d，正确；
③若a＞b，c＞d，取a=2，b=1，c=-2，d=-3，则ac＜bd，不成立；
④若ac2＞bc2，则a＞b，正确．
其中真命题的序号是②④．
故选：B．
点评：本题考查了不等式的基本性质，属于基础题．
练习册系列答案
相关题目
若数列{an}满足a1=1，a2=2，且an=
（n≥3），则a2010为（ ）
| an-1 |
| an-2 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、22010 |
方程x2+y2+2ax-by+c=0表示圆心为C（2，3），半径为3的圆，则a、b、c的值依次为（ ）
| A、2、6、4 |
| B、-2、6、4 |
| C、2、-6、4 |
| D、2、-6、-4 |
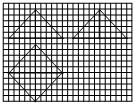一个几何体的三视图如图所示，其中网格纸上的小正方形的边长为1，则该几何体的体积为