题目内容
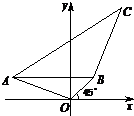 如图,在平面直角坐标系xOy中,已知点A(-3,1),直线OB的倾斜角为45°,且|OB|=
如图,在平面直角坐标系xOy中,已知点A(-3,1),直线OB的倾斜角为45°,且|OB|=| 2 |
(Ⅰ)求点B的坐标及线段AB的长度;
(Ⅱ)在平面直角坐标系xOy中,取1厘米为单位长度.现有一质点P以1厘米/秒的速度从点B出发,沿倾斜角为60°的射线BC运动,另一质点Q同时以
| 2 |
考点:解三角形的实际应用
专题:应用题,解三角形
分析:(Ⅰ)利用直线OB的倾斜角为45°,且|OB|=
,求点B的坐标,根据AB∥x轴求出线段AB的长度;
(Ⅱ)在△ABC中,由余弦定理知|AC|2=|AB|2+|BC|2-2|AB||BC|cos120°,建立方程,即可得出结论.
| 2 |
(Ⅱ)在△ABC中,由余弦定理知|AC|2=|AB|2+|BC|2-2|AB||BC|cos120°,建立方程,即可得出结论.
解答:
 解:(Ⅰ)设点B(x0,y0),依题意x0=
解:(Ⅰ)设点B(x0,y0),依题意x0=
cos45°=1,y0=
sin45°=1.
从而B(1,1),
又A(-3,1),所以AB∥x轴,则|AB|=|1-(-3)|=4.…(3分)
(Ⅱ)设质点Q与P经过t秒会合于点C,
则|AC|=
t,|BC|=t.
由AB∥x轴及BC的倾斜角为60°,得∠ABC=120°.
在△ABC中,由余弦定理知|AC|2=|AB|2+|BC|2-2|AB||BC|cos120°,
所以2t2=16+t2+8t•
,化简得,t2-4t-16=0,
解得t=2-2
(舍去)或t=2+2
.
答:若要使得质点Q与P会合,则需要经过(2+2
)秒.…(9分)
 解:(Ⅰ)设点B(x0,y0),依题意x0=
解:(Ⅰ)设点B(x0,y0),依题意x0=| 2 |
| 2 |
从而B(1,1),
又A(-3,1),所以AB∥x轴,则|AB|=|1-(-3)|=4.…(3分)
(Ⅱ)设质点Q与P经过t秒会合于点C,
则|AC|=
| 2 |
由AB∥x轴及BC的倾斜角为60°,得∠ABC=120°.
在△ABC中,由余弦定理知|AC|2=|AB|2+|BC|2-2|AB||BC|cos120°,
所以2t2=16+t2+8t•
| 1 |
| 2 |
解得t=2-2
| 5 |
| 5 |
答:若要使得质点Q与P会合,则需要经过(2+2
| 5 |
点评:本题考查解三角形的实际应用,考查学生的计算能力,正确运用余弦定理是关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
曲线y=
x3+
在点(2,4)处的切线方程是( )
| 1 |
| 3 |
| 4 |
| 3 |
| A、x+4y-4=0 |
| B、x-4y-4=0 |
| C、4x+y-4=0 |
| D、4x-y-4=0 |
方程x2+y2+2ax-by+c=0表示圆心为C(2,3),半径为3的圆,则a、b、c的值依次为( )
| A、2、6、4 |
| B、-2、6、4 |
| C、2、-6、4 |
| D、2、-6、-4 |
在△ABC中,A=60°,b=1,其面积为
,则c等于( )
| 3 |
| A、5 | ||
B、
| ||
| C、4 | ||
| D、3 |
设a>0,b>0且a+b=1则
+
的最小值是( )
| 1 |
| a |
| 2 |
| b |
| A、2 | ||
| B、4 | ||
C、3+2
| ||
| D、6 |
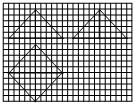 一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为1,则该几何体的体积为
一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为1,则该几何体的体积为