题目内容
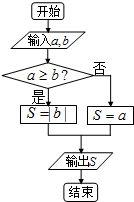 定义某种运算⊕,a⊕b的运算原理如图所示,设S=1⊕x,x∈[-2,2],则输出的S的最大值与最小值的差为( )
定义某种运算⊕,a⊕b的运算原理如图所示,设S=1⊕x,x∈[-2,2],则输出的S的最大值与最小值的差为( )| A、2 | B、-1 | C、4 | D、3 |
考点:程序框图
专题:函数的性质及应用,算法和程序框图
分析:通过程序框图判断出S=a?b的解析式,再求出f(x)的解析式,从而求出f(x)的解析式,即可得到函数的最大值与最小值的差.
解答:
 解:由流程图可得a?b=
解:由流程图可得a?b=
∴f(x)=1?x=
,画出它的图象,如图.
又∵x∈[-2,2],
当-2≤x≤1时,函数值y∈[0,2];
当1<x≤2时,函数值y=1,
∴分段函数的值域为[0,2].
∴f(x)的最大值为2.最小值为0.
∴S的最大值与最小值的差为2.
故选:A.
 解:由流程图可得a?b=
解:由流程图可得a?b=
|
∴f(x)=1?x=
|
又∵x∈[-2,2],
当-2≤x≤1时,函数值y∈[0,2];
当1<x≤2时,函数值y=1,
∴分段函数的值域为[0,2].
∴f(x)的最大值为2.最小值为0.
∴S的最大值与最小值的差为2.
故选:A.
点评:本题考查选择结构,主要考查了判断程序框图的功能即判断出新运算法则,利用运算法则求值.解决新定义题关键是理解题中给的新定义,属于基本知识的考查.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
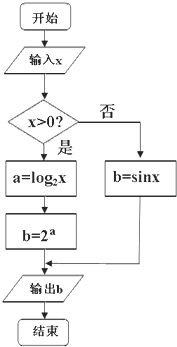 如图所示的程序框图,若两次输入的x值分别是3π和-
如图所示的程序框图,若两次输入的x值分别是3π和-| π |
| 3 |
A、1,
| ||||
B、0,
| ||||
C、-π,-
| ||||
D、3π,-
|
下列函数中,二次函数是( )
| A、y=8x2+1 | ||
| B、y=8x+1 | ||
C、y=
| ||
D、y=
|
若定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,则有( )
| A、f(-25)<f(80)<f(11) |
| B、f(11)<f(80)<f(-25) |
| C、f(-25)<f(11)<f(80) |
| D、f(80)<f(11)<f(-25) |
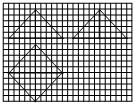 一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为1,则该几何体的体积为
一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为1,则该几何体的体积为