题目内容
有一半径为4的圆，现将一枚直径为2的硬币投向其中（硬币与圆面有公共点就算是有效试验，硬币完全落在圆外的不计），则硬币完全落入圆内的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：
分析：根据题意，算出硬币完全落入小圆内的事件对应的图形面积，以及所有基本事件对应图形的面积，结合几何概型计算公式即可算出所求的概率．
解答：
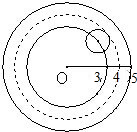解：记“硬币完全落入小圆内”为事件A，
事件A对应的图形是硬币圆心与纸板的圆心距离小于3的圆内，其面积为9π
而所有的基本事件对应的图形是硬币圆心与纸板的圆心距离小于5的圆内，其面积为25π
∴硬币完全落入小圆内的概率为P（A）=
．
故选D．
解：记“硬币完全落入小圆内”为事件A，事件A对应的图形是硬币圆心与纸板的圆心距离小于3的圆内，其面积为9π
而所有的基本事件对应的图形是硬币圆心与纸板的圆心距离小于5的圆内，其面积为25π
∴硬币完全落入小圆内的概率为P（A）=
| 9 |
| 25 |
故选D．
点评：本题给出硬币落入圆开纸板内的事件，求硬币完全落入小圆内的概率．着重考查了圆的面积公式和几何概型计算公式等知识，属于中档题．
练习册系列答案
孟建平名校考卷系列答案
相关题目
设a＞0，b＞0且a+b=1则
+
的最小值是（ ）
| 1 |
| a |
| 2 |
| b |
| A、2 | ||
| B、4 | ||
C、3+2
| ||
| D、6 |
若定义在R上的奇函数f（x）满足f（x-4）=-f（x），且在区间[0，2]上是增函数，则有（ ）
| A、f（-25）＜f（80）＜f（11） |
| B、f（11）＜f（80）＜f（-25） |
| C、f（-25）＜f（11）＜f（80） |
| D、f（80）＜f（11）＜f（-25） |
“x=-2”是“x≠0”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
| 1 |
| 2 |
| A、2+2i | B、2-2i |
| C、i | D、-i |