题目内容
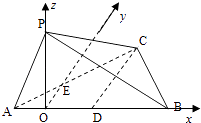
【题目】如图,在三棱锥P﹣ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC. 
(1)求直线PC与平面ABC所成角的大小;
(2)求二面角B﹣AP﹣C的大小.
【答案】
(1)解:[解法一]
设AB中点为D,AD中点为O,连接OC,OP,CD.
因为AB=BC=CA,所以CD⊥AB,
因为∠APB=90°,∠PAB=60°,所以△PAD为等边三角形,所以PO⊥AD,又平面PAB⊥平面ABC,平面PAB∩平面ABC=AD.
PO⊥平面ABC,∠OCP为直线PC与平面ABC所成的角
不妨设PA=2,则OD=1,OP= ![]() ,AB=4.
,AB=4.
所以CD=2 ![]() ,OC=
,OC= ![]() =
= ![]() =
= ![]()
在RT△OCP中,tan∠OCP= ![]() =
= ![]() =
= ![]() .
.
故直线PC与平面ABC所成的角的大小为arctan ![]() .
.
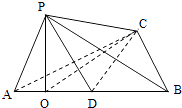
[解法二]
设AB中点为D,连接CD.因为O在AB上,且O为P在平面ABC内的射影,
所以PO⊥平面ABC,所以PO⊥AB,且PO⊥CD.因为AB=BC=CA,所以CD⊥AB,设E为AC中点,则EO∥CD,从而OE⊥PO,OE⊥AB.
如图,以O为坐标原点,OB,OE,OP所在直线分别为x,y,z轴建立空间直角坐标系O﹣xyz.不妨设PA=2,由已知可得,AB=4,OA=OD=1,OP= ![]() ,
,
CD=2 ![]() ,所以O(0,0,0),A(﹣1,0,0),C(1,2
,所以O(0,0,0),A(﹣1,0,0),C(1,2 ![]() ,0),P(0,0,
,0),P(0,0, ![]() ),所以
),所以 ![]() =(﹣1,﹣2
=(﹣1,﹣2 ![]() ,
, ![]() )
) ![]() =(0,0,
=(0,0, ![]() )为平面ABC的一个法向量.
)为平面ABC的一个法向量.
设α为直线PC与平面ABC所成的角,则sinα= 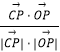 =
= ![]() =
= ![]() .故直线PC与平面ABC所成的角大小为arcsin
.故直线PC与平面ABC所成的角大小为arcsin ![]()
(2)解:[解法一]
过D作DE⊥AP于E,连接CE.
由已知,可得CD⊥平面PAB.根据三垂线定理知,CE⊥PA.所以∠CED为二面角
B﹣AP﹣C的平面角.由(1)知,DE= ![]() ,在RT△CDE中,tan∠CED=
,在RT△CDE中,tan∠CED= ![]() =
= ![]() =2,故二面角B﹣AP﹣C的大小为arctan2.
=2,故二面角B﹣AP﹣C的大小为arctan2.
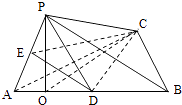
[解法二]
由(1)知, ![]() =(1,0,
=(1,0, ![]() ),
), ![]() =(2,2
=(2,2 ![]() ,0).
,0).
设平面APC的一个法向量为 ![]() =(x,y,z),则由
=(x,y,z),则由 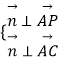 得出
得出 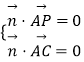 即
即 ![]() ,
,
取x=﹣ ![]() ,则y=1,z=1,所以
,则y=1,z=1,所以 ![]() =(﹣
=(﹣ ![]() ,1,1).设二面角B﹣AP﹣C的平面角为β,易知β为锐角.
,1,1).设二面角B﹣AP﹣C的平面角为β,易知β为锐角.
而面ABP的一个法向量为 ![]() =(0,1,0),则cosβ=
=(0,1,0),则cosβ= ![]() =
= ![]() =
= ![]() .
.
故二面角B﹣AP﹣C的大小为arccos ![]() .
.
【解析】解法一(1)设AB中点为D,AD中点为O,连接OC,OP,CD.可以证出∠OCP为直线PC与平面ABC所成的角.不妨设PA=2,则OD=1,OP= ![]() ,AB=4.在RT△OCP中求解.(2)以O为原点,建立空间直角坐标系,利用平面APC的一个法向量与面ABP的一个法向量求解.解法二(1)设AB中点为D,连接CD.以O为坐标原点,OB,OE,OP所在直线分别为x,y,z轴建立空间直角坐标系O﹣xyz.利用
,AB=4.在RT△OCP中求解.(2)以O为原点,建立空间直角坐标系,利用平面APC的一个法向量与面ABP的一个法向量求解.解法二(1)设AB中点为D,连接CD.以O为坐标原点,OB,OE,OP所在直线分别为x,y,z轴建立空间直角坐标系O﹣xyz.利用 ![]() 与平面ABC的一个法向量夹角求解.(2)分别求出平面APC,平面ABP的一个法向量,利用两法向量夹角求解.
与平面ABC的一个法向量夹角求解.(2)分别求出平面APC,平面ABP的一个法向量,利用两法向量夹角求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】“微信运动”是由腾讯开发的一个类似计步数据库的公众账号.用户可以通过关注“微信运动”公众号查看自己及好友每日行走的步数、排行榜,也可以与其他用户进行运动量的![]() 或点赞.现从某用户的“微信运动”朋友圈中随机选取40人,记录他们某一天的行走步数,并将数据整理如下:
或点赞.现从某用户的“微信运动”朋友圈中随机选取40人,记录他们某一天的行走步数,并将数据整理如下:
步数/步 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | 10000以上 |
男性人数/人 | 1 | 6 | 9 | 5 | 4 |
女性人数/人 | 0 | 3 | 6 | 4 | 2 |
规定:用户一天行走的步数超过8000步时为“运动型”,否则为“懈怠型”.
(1)将这40人中“运动型”用户的频率看作随机抽取1人为“运动型”用户的概率.从该用户的“微信运动”朋友圈中随机抽取4人,记![]() 为“运动型”用户的人数,求
为“运动型”用户的人数,求![]() 和
和![]() 的数学期望;
的数学期望;
(2)现从这40人中选定8人(男性5人,女性3人),其中男性中“运动型”有3人,“懈怠型”有2人,女性中“运动型”有2人,“懈怠型”有1人.从这8人中任意选取男性3人、女性2人,记选到“运动型”的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力.某移动支付公司从我市移动支付用户中随机抽取100名进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
合计 | 15 | 12 | 13 | 7 | 8 | 45 |
(Ⅰ)把每周使用移动支付超过3次的用户称为“移动支付活跃用户”,由以上数据完成下列![]() 列联表,并判断能否在犯错误的概率不超过0.005的前提下,认为“移动支付活跃用户”与性别有关?
列联表,并判断能否在犯错误的概率不超过0.005的前提下,认为“移动支付活跃用户”与性别有关?
移动支付活跃用户 | 非移动支付活跃用户 | 总计 | |
男 | |||
女 | |||
总计 | 100 |
(Ⅱ)把每周使用移动支付6次及6次以上的用户称为“移动支付达人”.为了做好调查工作,决定用分层抽样的方法从“移动支付达人”中抽取6人进行问卷调查,再从这6人中选派2人参加活动.求参加活动的2人性别相同的概率?
附公式及表如下:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |



