Question

【题目】已知定义域为的函数在上有最大值1，设 ．

（1）求的值；

（2）若不等式在上恒成立，求实数的取值范围；

（3）若函数有三个不同的零点，求实数的取值范围（为自然对数的底数）．

Answer 1

【答案】（1）0；（2）；（3）

【解析】

（1）结合二次函数的性质 可判断g（x）在[1，2]上的单调性，结合已知函数的最大值可求m；（2）由（1）可知f（x），由原不等式可知2k1在x∈[3，9]上恒成立，结合对数与二次函数的性质可求；（3）原方程可化为|ex﹣1|2﹣（3k+2）|ex﹣1|+（2k+1）＝0，利用换元q＝|ex﹣1|，结合二次函数的 实根分布即可求解．

（1）因为在上是增函数，

所以，解得．

（2）由（1）可得：

所以不等式在上恒成立．

等价于在上恒成立

令，因为，所以

则有在恒成立

令，，则

所以，即，所以实数的取值范围为．

（3）因为

令，由题意可知

令，

则函数有三个不同的零点

等价于在有两个零点，

当 ，此时方程，此时关于方程有三个零点，符合题意；

当 记为，，且，，

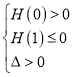所以，解得

综上实数的取值范围 ．