题目内容
14.已知函数f(x)=lnx+$\frac{a}{x}$-1(a∈R)(Ⅰ)讨论函数f(x)的单调性
(Ⅱ)求证:ln2•ln3•ln4•…•lnn>$\frac{1}{n}$(n≥2,n∈N*)
分析 (Ⅰ)先求出函数的导数,通过讨论a的范围,从而求出函数的单调区间;
(Ⅱ)将a=1代入函数的表达式,求出函数f(x)的极小值,得到lnx>1-$\frac{1}{x}$,分别令x=2,3,4,…,n,从而证出结论.
解答 解:(Ⅰ)f′(x)=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$=$\frac{x-a}{{x}^{2}}$,
当a≤0时,f′(x)>0,f(x)在(0,+∞)单调递增,
当a>0时,x∈(0,a),f′(x)<0,f(x)单调递减,
x∈(a,+∞),f′(x)>0,f(x)单调递增;
(Ⅱ)令a=1,则f(x)=lnx+$\frac{1}{x}$-1,(x>0),
由(Ⅰ)得:f(x)极小值=f(x)min=f(1)=0,
则x∈[2,+∞)时,f(x)>0,即lnx>1-$\frac{1}{x}$,
令x=n,则lnn>1-$\frac{1}{n}$=$\frac{n-1}{n}$,
∴ln2>$\frac{1}{2}$,ln3>$\frac{2}{3}$,ln4>$\frac{3}{4}$,…,lnn>$\frac{n-1}{n}$,
把以上n-1个式子相乘,则得到:
ln2•ln3•ln4…lnn>$\frac{1}{2}$•$\frac{2}{3}$•$\frac{3}{4}$…$\frac{n-1}{n}$=$\frac{1}{n}$.
点评 本题考察了函数的单调性,导数的应用,(Ⅱ)问中得到lnx>1-$\frac{1}{x}$是解题的关键,本题是一道中档题.

练习册系列答案
相关题目
4.已知函数y=f(x)的定义域是[0,2],那么g(x)=$\frac{f({x}^{2})}{1+lg(x+1)}$的定义域是( )
| A. | (-$\frac{9}{10}$,$\sqrt{2}$)∪(-1,-$\frac{9}{10}$) | B. | (-1,$\sqrt{2}$] | C. | (-1,-$\frac{9}{10}$) | D. | (-$\frac{9}{10}$,$\sqrt{2}$) |
19.执行如图所示的程序框图,则输出的S=( )
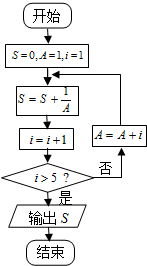

| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{8}{5}$ | D. | $\frac{12}{7}$ |
6.已知集合$A=\left\{{x\left|{y=\sqrt{1-x}}\right.}\right\}$,B={x|1≤3x≤9},则A∩B=( )
| A. | [-1,0] | B. | [0,1] | C. | [-1,2] | D. | [1,2] |
4.若曲线y2=2px(p>0)上有且只有一个点到其焦点的距离为1,则p的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
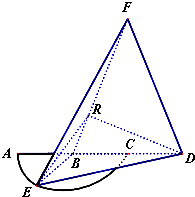 如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.
如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.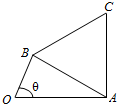 已知函数f(x)=sinωx(0<ω<2)在区间,[0,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3}$,$\frac{2π}{3}$]单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$.
已知函数f(x)=sinωx(0<ω<2)在区间,[0,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3}$,$\frac{2π}{3}$]单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$.