题目内容

20．已知函数f（x）=cos2x-$\frac{1}{2}$，则（　　）
A．f（x）为偶函数且最小正周期为πB．f（x）为奇函数且最小正周期为π
C．f（x）为偶函数且最小正周期为2πD．f（x）为奇函数且最小正周期为2π

分析 由二倍角的余弦函数公式化简可得f（x）=$\frac{1}{2}$cos2x，由余弦函数的图象和性质即可得解．

解答 解：∵f（x）=cos2x-$\frac{1}{2}$=$\frac{1+cos2x}{2}$-$\frac{1}{2}$=$\frac{1}{2}$cos2x，
∴T=$\frac{2π}{2}$=π，
∴由余弦函数的图象和性质可知f（x）为偶函数且最小正周期为π．
故选：A．

点评 本题主要考查了二倍角的余弦公式，三角函数的周期性及其求法，余弦函数的图象和性质，属于基础题．

练习册系列答案
相关题目
10．已知函数p（x）=lnx+1，q（x）=ex，若q（x1）=p（x2）成立，则x2-x1的最小值为1．
11．设直线x+y=1与抛物线y2=2px（p＞0）交于A，B两点，若OA⊥OB，则△OAB的面积为（　　）
A．1B．$\frac{1}{2}\sqrt{5}$C．$\sqrt{5}$D．2
8．若某几何体的三视图是如图所示的三个直角三角形，则该几何体的外接球的表面积为50π．
15．数列{an}满足a1∈（0，1），an+1=-a${\;}_{n}^{2}$+an+c（n∈N*）
（1）证明：“对任意a1∈（0，1），an∈（0，1）”的充要条件是“c∈[0，$\frac{3}{4}$）”
（2）若a1=$\frac{1}{5}$，c=0，数列{bn}满足bn=$\frac{1}{1-{a}_{n}}$，设Tn=b1+b2+…+bn，Rn=b1•b2…bn，若对任意的n≥10，
n∈N*，不等式kn-n2（5Rn-Tn）≥2015的解集非空，求满足条件的实数k的最小值．
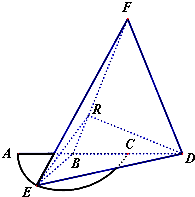5．如图，弧$\widehat{AEC}$是半径为a的半圆，AC为直径，点E为弧$\widehat{AC}$的中点，点B和点C为线段AD的三等分点，平面AEC外一点F满足FB=FD=$\sqrt{5}$a，FE=$\sqrt{6}$a．
（Ⅰ）证明：EB⊥FD；
（Ⅱ）已知点R为线段FB上的点，且FR=λFB，求当RD最短时，直线RE和平面BDE所成的角的正弦值．
12．已知函数f（x）=（2-a）lnx+$\frac{1}{x}$+2ax（a∈R）．
（Ⅰ）当a＜0时，求f（x）的单调区间；
（Ⅱ）实数m为何值时，对任意的a∈（-3，-2）及x1，x2∈[1，3]，恒有|f（x1）-f（x2）|＜（m+ln3）a-2ln3成立．
9．已知函数f（x）=$\left\{{\begin{array}{l}{x+\frac{1}{x}，x＞0}\\{{x^3}+3，x≤0}\end{array}}$，当2＜a≤3时，则方程f（2x2+x）=a的根最多个数是（　　）
A．4B．5C．6D．7
10．已知正实数a，b满足：a+b=2．
（Ⅰ）求$\frac{1}{a}+\frac{1}{b}$的最小值m；
（Ⅱ）设函数f（x）=|x-t|+|x+$\frac{1}{t}$|（t≠0），对于（Ⅰ）中求得的m，是否存在实数x，使得f（x）=m成立，若存在，求出x的取值范围，若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网