题目内容
11．已知正数x，y满足$\left\{\begin{array}{l}{2x-y≤0}\\{x-3y+5≥0}\end{array}\right.$，则z=-2x-y的最小值为（ ）| A． | -5 | B． | 5 | C． | 4 | D． | -4 |
分析 首先画出平面区域，然后根据z的几何意义求最小值．
解答 解：由已知正数x，y满足$\left\{\begin{array}{l}{2x-y≤0}\\{x-3y+5≥0}\end{array}\right.$，对应的区域如图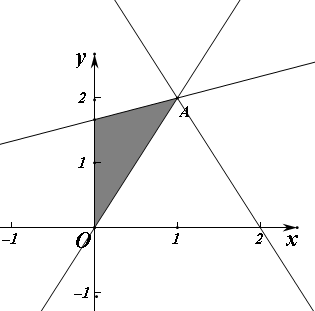
解$\left\{\begin{array}{l}{2x-y=0}\\{x-3y+5=0}\end{array}\right.$得A（1，2）
当直线z=-2x-y经过A时最小为-2-2=-4．
故选D．
点评 本题考查了简单线性规划问题；一般步骤是画出约束条件对应的区域，根据目标函数的几何意义求最值；体现了数形结合的思想．
练习册系列答案
相关题目
4．利用计算器算出自变量和函数值的对应值如表，则方程2x-x2=0的一个根所在区间为（1.8，2.2）．
| x | 0.2 | 0.6 | 1.0 | 1.4 | 1.8 | 2.2 | 2.6 | 3.0 | 3.4 | … |
| y=2x | 1.149 | 1.516 | 2.0 | 2.639 | 3.482 | 4.595 | 6.063 | 8.0 | 10.556 | … |
| y=x2 | 0.04 | 0.36 | 1.0 | 1.96 | 3.24 | 4.84 | 6.76 | 9.0 | 11.56 | … |
6．已知{an}为等差数列，若a1+a9=$\frac{π}{3}$，则cos（a3+a7）的值为（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
，若关于
的方程
有且只有四个不相等的实数根，则实数
的取值范围是____________．
19．为考察高中生的性别与是否喜欢数学课程之间的关系，在某城市的某校高中生中随机抽取100名学生，其中男生喜欢数学课程的20人，不喜欢数学课程的30人；女生喜欢数学课程的10人，不喜欢数学课程的40人．
（Ⅰ）根据以上数据作2×2列联表；（答案填写在答题纸上）
（Ⅱ）根据以上数据，能否有95%的把握认为“高中生的性别与是否喜欢数学课程有关”？
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+b）（b+d）}$．
（Ⅰ）根据以上数据作2×2列联表；（答案填写在答题纸上）
| 喜欢数学课程 | 不喜欢数学课程 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P（K2≥k） | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |