题目内容
13．以原点（0，0）为圆心，且与直线x+y-2=0相切的圆的方程为x2+y2=2．分析 根据题意得圆心到切线的距离即为圆的半径，利用点到直线的距离公式求出圆的半级，写出圆的标准方程即可．
解答 解：根据题意，圆的圆心到直线的距离，就是半径，
则r=$\frac{2}{\sqrt{{1}^{2}+{1}^{2}}}$=$\sqrt{2}$，
则圆的方程为x2+y2=2，
故答案为x2+y2=2．
点评 本题考查圆的方程的求法，涉及点到直线的距离，求出圆的半径是解本题的关键．
练习册系列答案
相关题目
3．观察数表：
1 2 3 4 …第一行
2 3 4 5 …第二行
3 4 5 6 …第三行
4 5 6 7 …第四行
…
第一列 第二列 第三列 第四列
根据数表中所反映的规律，第n行与第n-1列的交叉点上的数应该是（ ）
1 2 3 4 …第一行
2 3 4 5 …第二行
3 4 5 6 …第三行
4 5 6 7 …第四行
…
第一列 第二列 第三列 第四列
根据数表中所反映的规律，第n行与第n-1列的交叉点上的数应该是（ ）
| A． | 2n-1 | B． | 2n+1 | C． | n2-1 | D． | 2n-2 |
1．过圆x2+y2-4x+my=0上一点P（1，1）的圆的切线方程为（ ）
| A． | 2x+y-3=0 | B． | 2x-y-1=0 | C． | x-2y-1=0 | D． | x-2y+1=0 |
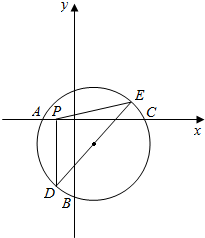如图，直角三角形ABC的顶点坐标A（-2，0）、B（0，$-2\sqrt{2}$），顶点C在x轴上，点P为线段OA的中点，设圆M是△ABC的外接圆，若DE是圆M的任意一条直径，试探究$\overrightarrow{PD}•\overrightarrow{PE}$是否是定值？若是，求出定值；若不是，请说明理由．
5．下列函数是奇函数的是（ ）
| A． | y=x2+1 | B． | y=sinx | C． | y=log2（x+5） | D． | y=2x-3 |
2．在△ABC中，∠A=60°，a=$\sqrt{14}$，b=4，满足条件的△ABC（ ）
| A． | 无解 | B． | 只有一解 | C． | 有两解 | D． | 不能确定 |