题目内容
2．在△ABC中，∠A=60°，a=$\sqrt{14}$，b=4，满足条件的△ABC（ ）| A． | 无解 | B． | 只有一解 | C． | 有两解 | D． | 不能确定 |
分析 根据正弦定理结合三角形有解的条件进行判断即可．
解答 解：C到AB边的高h=bsinA=4×sin60°=4×$\frac{\sqrt{3}}{2}$=$2\sqrt{3}$，
∵$2\sqrt{3}$＜$\sqrt{14}$＜4，
∴h＜a＜b，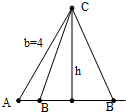
∴对应的三角形有两个，
法2：由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$，
则sinB=$\frac{bsinA}{a}$=$\frac{4×\frac{\sqrt{3}}{2}}{\sqrt{14}}$=$\frac{\sqrt{42}}{7}$，
∵b＞a，
∴B＞60°，
故B有一个为锐角，一个为钝角，
故选：C
点评 本题主要考查三角形个数的判断，根据a与h=bsinA的关系是解决本题的关键．
练习册系列答案
相关题目
17．已知向量$\overrightarrow{OA}$=（2，2），$\overrightarrow{OB}$=（4，1），在x轴上有一点P，使$\overrightarrow{AP}$•$\overrightarrow{BP}$有最小值，则P点坐标为（ ）
| A． | （-3，0） | B． | （3，0） | C． | （2，0） | D． | （4，0） |
如图，在四棱锥P-ABCD中，PD⊥平面ABCD，底面ABCD为平行四边形，∠ADB=90°，AB=2AD．
如图所示，在多面体A1B1D1-ABCD，四边形AA1B1B，ADD1A1，ABCD均为正方形，E为B1D1的中点，过A1，D，E的平面交CD1于F
11．在△ABC中，若sinA：sinB：sinC=2：3：4，则△ABC是（ ）
| A． | 直角三角形 | B． | 钝角三角形 | C． | 锐三角形 | D． | 等腰直角三角形 |