题目内容
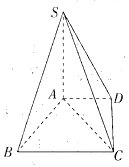
【题目】如图,在等腰三角形ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DBCE. 
(1)求证:△ADB∽△EAC;
(2)若∠BAC=40°,求∠DAE的度数.
【答案】
(1)证明:∵AB=AC,∴∠ABC=∠ACB,
∴∠ABD=∠ACE,
∵AB2=DBCE
∴ ![]() =
= ![]() ,
,
∵AB=AC,
∴ ![]() =
= ![]()
∴△ADB∽△EAC
(2)解:∵△ADB∽△EAC,∴∠BAD=∠E,∠D=∠CAE,
∵∠DAE=∠BAD+∠BAC+∠CAE,
∴∠DAE=∠D+∠BAD+∠BAC,
∵∠BAC=40°,AB=AC,
∴∠ABC=70°,
∴∠D+∠BAD=70°,
∴∠DAE=∠D+∠BAD+∠BAC=70°+40°=110°
【解析】(1)根据AB=AC,求得∠ABD=∠ACE,再利用AB2=DBCE,即可得出对应边成比例,然后即可证明.(2)由△ADB∽△EAC,得出∠BAD=∠E,∠D=∠CAE,则∠DAE=∠BAD+∠BAC+∠CAE=∠D+∠BAD+∠BAC,很容易得出答案.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目