Question

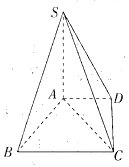
【题目】如图所示，四棱锥中，平面平面， ， ， ．

（1）证明：在线段上存在一点，使得平面；

（2）若，在（1）的条件下，求三棱锥的体积．

Answer 1

【答案】(1)见解析;(2) .

【解析】试题分析：（1）取的中点，易得：四边形是平行四边形，从而，所以平面；（2）∵是的中点，∴到平面的距离等于到平面的距离的一半从而易得三棱锥的体积.

试题解析：

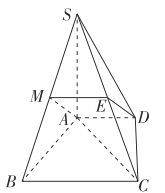
（1）如图，取的中点， 的中点，连接， ，

∵是的中位线，∴ ，

依题意得， ，则有 ，∴四边形是平行四边形，∴，

∵平面， 平面，∴平面．

（2）∵平面平面，平面平面， ， 平面，故平面，

∵是的中点，

∴到平面的距离等于到平面的距离的一半，且平面， ，

∴三棱锥的高是2， ，

在等腰中， ， ， 边上的高为，

，∴到的距离为，∴，

∴．