题目内容
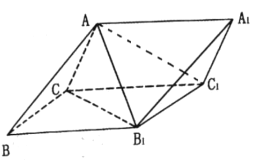
【题目】四棱锥S﹣ABCD中，底面ABCD为平行四边形，侧面SBC⊥面ABCD，已知∠ABC=45°，AB=2，BC=2 
，SB=SC= 
． 
（1）设平面SCD与平面SAB的交线为l，求证：l∥AB；
（2）求证：SA⊥BC；
（3）求直线SD与面SAB所成角的正弦值．
【答案】
（1）证明：∵底面ABCD为平行四边形，
∴AB∥CD，∵AB平面SCD，CD平面SCD，
∴AB∥平面SCD，又AB平面SAB，平面SCD∩平面SAB=l，
∴l∥AB．
（2）证明：取BC中点O，连接OS，OA．
∵OB= 
BC= 
，AB=2，∠ABC=45°，
∴OA= 
= ．
∴OA2+OB2=AB2，∴OA⊥BC．
∵SB=SC，O是BC的中点，∴OS⊥BC，
又SO平面SOA，OA平面SOA，SO∩OA=O，
∴BC⊥平面SOA，∵SA平面SOA，
∴BC⊥SA．
（3）解：∵SB=SC，O是BC中点，∴SO⊥BC．
∵侧面SBC⊥面ABCD，侧面SBC∩面ABCD=BC，
∴SO⊥平面ABCD．
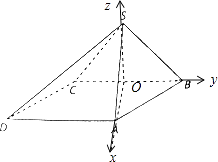
以O为原点，以OA，OB，OS为坐标轴建立空间直角坐标系O﹣xyz，如图所示，
则A（ ，0，0），B（0， ，0），S（0，0，1），D（ ，﹣2 ，0），
∴ 
=（ ，﹣2 ，﹣1）， 
=（ ，0，﹣1）， 
=（ ，﹣ ，0）．
设平面SAB法向量为 
=（x，y，z），则 
，
∴ 
．令x=1，则y=1，z= ，∴ =（1，1， ）．
∴cos＜ ， ＞= 
= 
= 
．
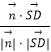∴直线SD与面SAB所成角的正弦值为 ．
【解析】
【考点精析】掌握棱锥的结构特征和空间角的异面直线所成的角是解答本题的根本，需要知道侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方；已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则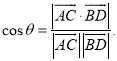
．
