Question

【题目】设函数f（x）=x2﹣aln（x+2），g（x）=xex ， 且f（x）存在两个极值点x1、x2 ， 其中x1＜x2 ．
（1）求实数a的取值范围；
（2）求g（x1﹣x2）的最小值；
（3）证明不等式：f（x1）+x2＞0．

Answer 1

【答案】
（1）解：由题：f′（x）=2x﹣ （x＞﹣2）．

∵f（x）存在两个极值点x1、x2，其中x1＜x2

∴关于x的方程2x﹣ =0，即2x2+4x﹣a=0在（﹣2，+∞）内有不等实根

令S（x）=2x2+4x（x＞﹣2），T（x）=a，

则﹣2＜a＜0，

∴实数a的取值范围是（﹣2，0）

（2）解：由（1）可知

∴g（x）=xex得g（x）=（x+1）ex

∴当x∈（﹣2，﹣1）时，g′（x）＜0，即g（x）在（﹣2，﹣1）单调递减；当x∈（﹣1，0）时，g′（x）＞0，即g（x）在（﹣1，0）单调递增

∴g（x1﹣x2）min=g（﹣1）=﹣

（3）证明：由（1）知 ，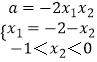

∴ =

令﹣x2=x，则0＜x＜1且

F（x）=﹣x﹣

F′（x）=﹣1+ （0＜x＜1）

∴G（x）= （0＜x＜1）

G′（x）=﹣ =

∵0＜x＜1，

∴G′（x）=﹣

∵0＜x＜1，∴G′（x）＜0，即F′（x）在（0，1）上是减函数．

∴F′（x）＞F′（1）＞0，

∴F（x）在（0，1）上是增函数

∴F（x）＜F（1）=﹣1，即 ，即f（x1）+x2＞0

【解析】（1）f（x）存在两个极值点，等价于其导函数有两个相异零点；（2）先找出（x1﹣x2）的取值范围，再利用g（x）的导函数可找出最小值；（3）适当构造函数，并注意x1与x2的关系，转化为函数求最大值问题，证明相关不等式．
【考点精析】关于本题考查的函数的极值与导数和函数的最大(小)值与导数，需要了解求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值；求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值才能得出正确答案．