题目内容
8.下列函数中,既不是奇函数,也不是偶函数的是( )| A. | y=x+sinx | B. | y=xsinx | C. | y=x+cosx | D. | y=xcosx |
分析 直接利用函数奇偶性的定义逐一判断四个选项得答案.
解答 解:函数y=f(x)=x+sinx的定义域为R,且f(-x)=-f(x),∴y=x+sinx为奇函数;
y=f(x)=xsinx的定义域为R,且f(-x)=f(x),∴y=xsinx为偶函数;
y=x+cosx的定义域为R,由f(-x)-f(x)=0,得-x+cosx-x-cosx=0,得x=0,不满足对任意x都成立,
由f(-x)+f(x)=0,得-x+cosx+x+cosx=0,得cosx=0,不满足对任意x都成立,
∴y=x+cosx为非奇非偶函数;
y=f(x)=xcosx的定义域为R,且f(-x)=-f(x),∴y=xcosx为奇函数.
故选:C.
点评 本题考查函数就偶性的性质,训练了函数奇偶性的判定方法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.圆心在y轴上,且过点(3,1)的圆与x轴相切,则该圆的方程是( )
| A. | x2+y2+10y=0 | B. | x2+y2-10y=0 | C. | x2+y2+10x=0 | D. | x2+y2-10x=0 |
19.己知0<a1<1,数列{an}满足:an+1=an-1+$\frac{n}{n{+}_{{a}_{n}}}$,n∈N+,则满足ai+aj(i<j,i,j∈N+)为整数的正整数组对(i,j)( )
| A. | 至多一对 | B. | 至多2对 | C. | 有无穷对 | D. | 不存在 |
16.已知全集U={1,2,3,4,5,6,7},A={2,4,6},B={1,3,5,6,7},则A∩(∁UB)等于( )
| A. | {2,4,6} | B. | {1,3,5} | C. | {2,4} | D. | {2,5} |
3.等差数列{an}中,a3=5,a4+a8=22,则{an}的前8项的和为( )
| A. | 32 | B. | 64 | C. | 108 | D. | 128 |
13.直线l:y=x-1的倾斜角是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{4}$ |
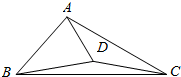 已知∠BAC>90°,∠ACB=30°,AB=DB=DC,求∠CAD的度数.
已知∠BAC>90°,∠ACB=30°,AB=DB=DC,求∠CAD的度数.