题目内容
9．已知正四面体的各棱长都为$\sqrt{2}$，四个顶点都在同一球面上，则该球的表面积为3π．分析 把四面体补成正方体，两者的外接球是同一个，求出正方体的棱长，然后求出正方体的对角线长，就是球的直径，即可得到答案．
解答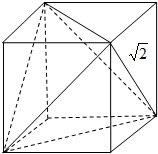 
解：如图，将四面体补成正方体，则正方体的棱长是1，正方体的对角线长为：$\sqrt{3}$
棱长都为$\sqrt{2}$的四面体的四个顶点在同一球面上，则正方体的八个顶点也在同一球面上，正方体的对角线就是球的直径．
则球的半径R=$\frac{\sqrt{3}}{2}$
∴球的表面积为3π，
故答案为：3π．
点评 本题考查球的体积，考查空间想象能力，正四面体的外接球转化为正方体外接球，使得问题的难度得到降低，问题得到解决，注意正方体的对角线就是球的直径，也是比较重要的．
练习册系列答案
相关题目
20．$\frac{7}{8}-\frac{7}{4}{sin^2}{15°}$的值等于（ ）
| A． | $\frac{7}{8}$ | B． | $\frac{7}{16}$ | C． | $\frac{{7\sqrt{3}}}{8}$ | D． | $\frac{{7\sqrt{3}}}{16}$ |
4．抛物线x2=-$\frac{1}{8}$y的准线方程是（ ）
| A． | x=$\frac{1}{16}$ | B． | y=$\frac{1}{16}$ | C． | y=$\frac{1}{32}$ | D． | x=$\frac{1}{32}$ |
18．圆心在y轴上，且过点（3，1）的圆与x轴相切，则该圆的方程是（ ）
| A． | x2+y2+10y=0 | B． | x2+y2-10y=0 | C． | x2+y2+10x=0 | D． | x2+y2-10x=0 |