题目内容
19.某商场向顾客甲、乙、丙随机发放红包,每次发放1个.(Ⅰ)若发放5元的红包2个,求甲恰得1个的概率;
(Ⅱ)若商场发放3个红包,其中5元的2个,10元的1个.记乙所得红包的总钱数为X,求X的分布列和期望.
分析 (Ⅰ)设“甲恰得一个红包”为事件A,利用独立重复试验求出概率即可.
(Ⅱ)X的所有可能值为0,5,10,15,20.求出概率的分布列,然后求解期望即可.
解答 解:(Ⅰ)设“甲恰得一个红包”为事件A,P(A)=${C}_{2}^{1}$×$\frac{1}{3}$×$\frac{2}{3}$=$\frac{4}{9}$.
(Ⅱ)X的所有可能值为0,5,10,15,20.
P(X=0)=($\frac{2}{3}$)2×$\frac{2}{3}$=$\frac{8}{27}$,P(X=5)=${C}_{2}^{1}$×$\frac{1}{3}$×($\frac{2}{3}$)2=$\frac{8}{27}$,
P(X=10)=($\frac{1}{3}$)2×$\frac{2}{3}$+($\frac{2}{3}$)2×$\frac{1}{3}$=$\frac{6}{27}$,P(X=15)=${C}_{2}^{1}$×($\frac{1}{3}$)2×$\frac{2}{3}$=$\frac{4}{27}$,
P(X=20)=($\frac{1}{3}$)3=$\frac{1}{27}$.
X的分布列:
| X | 0 | 5 | 10 | 15 | 20 |
| P | $\frac{8}{27}$ | $\frac{8}{27}$ | $\frac{6}{27}$ | $\frac{4}{27}$ | $\frac{1}{27}$ |
点评 本题考查离散型随机变量的分布列,期望的求法,考查概率求解的方法.

练习册系列答案
相关题目
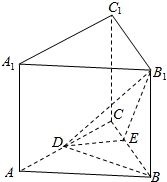 在正三棱柱ABC-A1B1C1中,AB=4,AA1=3,点D是AC的中点,点E在棱BC上(不含端点),且DE⊥B1E.
在正三棱柱ABC-A1B1C1中,AB=4,AA1=3,点D是AC的中点,点E在棱BC上(不含端点),且DE⊥B1E.