题目内容
【题目】已知函数![]() (
(![]() ).
).
(1)若曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(2)若对于任意![]() 且
且![]() ,都有
,都有![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
(3)若对于任意![]() ,都有
,都有![]() 成立,求整数
成立,求整数![]() 的最大值.
的最大值.
(其中![]() 为自然对数的底数)
为自然对数的底数)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)由题意得:![]() ,由题意可得
,由题意可得![]() ,解得
,解得![]() .
.
(2)因为![]() ,所以
,所以![]() ,
,
记![]() ,可知
,可知![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,记
上恒成立,记![]() ,即可求得
,即可求得![]() 的取值范围.
的取值范围.
(3)若对于任意![]() ,都有
,都有![]() 成立,
成立,
所以![]() 对于任意
对于任意![]() 恒成立,
恒成立,
即![]() 对于任意
对于任意![]() 恒成立,
恒成立,
令![]() ,利用导数研究函数
,利用导数研究函数![]() 的性质,即可得到整数
的性质,即可得到整数![]() 的最大值.
的最大值.
详解:
(1)由题意得:![]() ,
,
又曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,
平行,
所以![]() ,解得
,解得![]() .
.
(2)因为![]() ,所以
,所以![]() ,
,
记![]() ,又因为
,又因为![]() 且
且![]() ,
,
所以![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,记
上恒成立,记![]() ,
,
所以![]() ,令
,令![]() ,解得
,解得![]() ,
,
因为当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以当![]() 时,
时,![]() 取到最大值
取到最大值![]() ,
,
所以![]() .
.
(3)若对于任意![]() ,都有
,都有![]() 成立,
成立,
所以![]() 对于任意
对于任意![]() 恒成立,
恒成立,
即![]() 对于任意
对于任意![]() 恒成立,
恒成立,
令![]() ,所以
,所以![]() ,
,
再令![]() ,所以
,所以![]() 在
在![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,![]() ,
,
所以必存在唯一的解![]() ,使得
,使得![]() ,
,
即![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以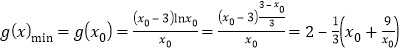 ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() 的最大整数为
的最大整数为![]() ,
,
所以整数![]() 的最大值为
的最大值为![]() .
.

【题目】已知函数 ![]() (
( ![]() ),若函数F(x)=f(x)﹣3的所有零点依次记为x1 , x2 , x3 , …,xn , 且x1<x2<x3<…<xn , 则x1+2x2+2x3+…+2xn﹣1+xn= .
),若函数F(x)=f(x)﹣3的所有零点依次记为x1 , x2 , x3 , …,xn , 且x1<x2<x3<…<xn , 则x1+2x2+2x3+…+2xn﹣1+xn= .
【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:
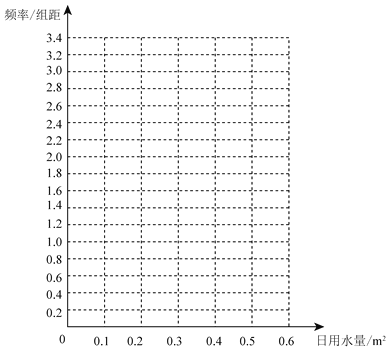
(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)