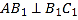题目内容
【题目】已知函数 
（ 
），若函数F（x）=f（x）﹣3的所有零点依次记为x1 ， x2 ， x3 ， …，xn ， 且x1＜x2＜x3＜…＜xn ， 则x1+2x2+2x3+…+2xn﹣1+xn= ．
【答案】445π
【解析】解：令2x+ 
= 
+kπ得x= + 
，k∈Z，即f（x）的对称轴方程为x= + ，k∈Z． ∵f（x）的最小正周期为T=π， 
，
∴f（x）在（0， 
）上有30条对称轴，
∴x1+x2=2× ，x2+x3=2× 
，x3+x4=2× 
，…，xn﹣1+xn=2× 
，
将以上各式相加得：x1+2x2+2x3+…+2xn﹣1+xn=2×（ + + +…+ ）=2× 
×30=445π．
所以答案是：445π．
练习册系列答案
科学实验活动册系列答案
相关题目
【题目】随着人们经济收入的不断增长，个人购买家庭轿车已不再是一种时尚．车的使用费用，尤其是随着使用年限的增多，所支出的费用到底会增长多少，一直是购车一族非常关心的问题．某汽车销售公司做了一次抽样调查，并统计得出某款车的使用年限
（单位：年）与所支出的总费用
（单位：万元）有如下的数据资料：
使用年限 | 2 | 3 | 4 | 5 | 6 |
总费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知对呈线性相关关系．
线性回归方程系数公式：
，
.
（1）试求线性回归方程
的回归系数
，
；
（2）当使用年限为10年时，估计车的使用总费用．
