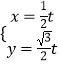Question

【题目】已知函数f（x）=2cos22x﹣2，给出下列命题： ①β∈R，f（x+β）为奇函数；
②α∈（0， ），f（x）=f（x+2α）对x∈R恒成立；
③x1 ， x2∈R，若|f（x1）﹣f（x2）|=2，则|x1﹣x2|的最小值为 ；
④x1 ， x2∈R，若f（x1）=f（x2）=0，则x1﹣x2=kπ（k∈Z）．其中的真命题有（ ）
A.①②
B.③④
C.②③
D.①④

Answer 1

【答案】C
【解析】解：由题意，f（x）=2cos22x﹣2=cos4x﹣1；

对于①，∵f（x）=cos4x﹣1的图象如图所示：

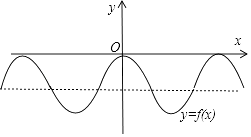
函数f（x+β）的图象是f（x）的图象向左或向右平移|β|个单位，

它不会是奇函数的，故①错误；

对于②，f（x）=f（x+2α），∴cos4x﹣1=cos（4x+8α）﹣1，

∴8α=2kπ，∴α= ，k∈Z；

又α∈（0， ），∴取α= 或 时，

∴f（x）=f（x+2α）对x∈R恒成立，②正确；

对于③，|f（x1）﹣f（x2）|=|cos4x1﹣cos4x2|=2时，

|x1﹣x2|的最小值为 = = ，∴③正确；

对于④，当f（x1）=f（x2）=0时，

x1﹣x2=kT=k = （k∈Z），∴④错误；

综上，真命题是②③．

故选：C．

化简函数f（x），画出f（x）的图象，根据图象平移判断函数f（x+β）不是奇函数，判断①错误；

根据f（x）=f（x+2α）求出方程在α∈（0， ）的解，判断②正确；

由|f（x1）﹣f（x2）|=2时，|x1﹣x2|的最小值为 = ，判断③正确；

当f（x1）=f（x2）=0时，x1﹣x2=kT= ，判断④错误．