题目内容
3.如图数阵中的前n行的数字和为2n+2-2n-4;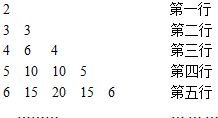
分析 由已知中数阵,分析其与杨徽三角的关系,先求出第n行的数字和,再利用分组求和法,结合等比数列的前n项和公式,可得答案.
解答 解:由已知中数阵: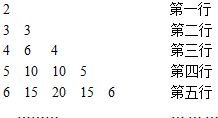
可知:该数阵是杨徽三角去掉每一行的第一个数字和最后一个数字(均为1)所得,
即第n行的数字均为(x+y)n+1展开式中,除了第一项和最后一项的系数,
令x=y=1,则第n行的数字和2n+1-2,
故前n行的数字和为(22-2)+(23-2)+(24-2)+…+(2n+1-2)=2n+2-2n-4,
故答案为:2n+2-2n-4.
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
14.以双曲线$\frac{{x}^{2}}{10}$-$\frac{{y}^{2}}{15}$=1的右焦点为圆心,且与其渐近线相切的圆的方程是( )
| A. | x2+y2-10x+10=0 | B. | x2+y2-10x+15=0 | C. | x2+y2+10x+15=0 | D. | x2+y2+10x+10=0 |
18.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $2\sqrt{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 4 |
12.设i是虚数单位,a为实数,复数z=$\frac{1+ai}{i}$为纯虚数,则z的共轭复数为( )
| A. | -i | B. | i | C. | 2i | D. | -2i |