题目内容
10．已知抛物线x2=-4$\sqrt{5}$y的焦点与双曲线$\frac{x^2}{a}+\frac{y^2}{4}$=1（a∈R）的一焦点重合，则该双曲线的离心率为（ ）| A． | $\frac{{\sqrt{5}}}{2}$ | B． | $\sqrt{5}$ | C． | $\frac{{5\sqrt{3}}}{3}$ | D． | $\frac{{3\sqrt{5}}}{5}$ |
分析 求出抛物线的焦点，即有双曲线的c=$\sqrt{5}$，a=2，再由离心率公式，即可得到．
解答 解：抛物线x2=-4$\sqrt{5}$y的焦点为（0，-$\sqrt{5}$），
则双曲线$\frac{x^2}{a}+\frac{y^2}{4}$=1（a∈R）的c=$\sqrt{5}$，a=2，
则离心率为e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$．
故选：A．
点评 本题考查抛物线和双曲线的方程和性质，考查离心率的求法，考查运算能力，属于基础题．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
1．已知函数f（x）=ln（ex+a）（a为常数）是实数R上的奇函数，若关于x的方程$\frac{lnx}{f（x）}$=x2-2ex+m的根的个数为2，则实数m的范围为（ ）
| A． | m≥e2+$\frac{1}{e}$ | B． | m＞$\frac{1}{e}$ | C． | m＜e2+$\frac{1}{e}$ | D． | m≤$\frac{1+e}{e}$ |
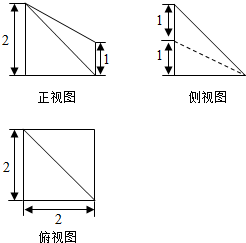
18．某几何体的三视图如图所示，则该几何体的体积为（ ）
| A． | $2\sqrt{2}$ | B． | $\frac{4}{3}$ | C． | $\frac{8}{3}$ | D． | 4 |