题目内容
设等差数列{an}的首项a1及公差d都为整数,前n项和为Sn.
(1)若a11=0,S14=98,求数列{an}的通项公式;
(2)若a1≥6,a11>0,S14≤77,求所有可能的数列{an}的通项公式.
(1)若a11=0,S14=98,求数列{an}的通项公式;
(2)若a1≥6,a11>0,S14≤77,求所有可能的数列{an}的通项公式.
(1)由S14=98,得2a1+13d=14,
又a11=a1+10d=0.
解得a1=20,d=-2,因此{an}的通项公式是
an=22-2n,(n=1,2,3,…).
(2)由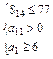 ,得
,得
即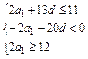 .
.
解得- ﹤d≤-
﹤d≤- ,又d∈Z,故d=-1.
,又d∈Z,故d=-1.
∴10<a1≤12,a1∈Z,故a1=11或a1=12.
所以,所有可能的数列{an}的通项公式是
an=12-n和an=13-n,(n=1,2,3…).
又a11=a1+10d=0.
解得a1=20,d=-2,因此{an}的通项公式是
an=22-2n,(n=1,2,3,…).
(2)由
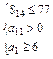 ,得
,得
即
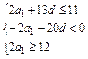 .
.解得-
 ﹤d≤-
﹤d≤- ,又d∈Z,故d=-1.
,又d∈Z,故d=-1.∴10<a1≤12,a1∈Z,故a1=11或a1=12.
所以,所有可能的数列{an}的通项公式是
an=12-n和an=13-n,(n=1,2,3…).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
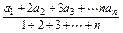 ,若{bn}为等差数列,求证:{an}也为等差数列.
,若{bn}为等差数列,求证:{an}也为等差数列.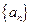 定义如下:
定义如下: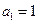 ,且当
,且当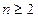 时,
时,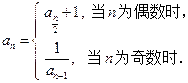
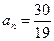 ,求正整数n.
,求正整数n.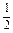 an-30,求数列{bn}的前n项和的最小值.
an-30,求数列{bn}的前n项和的最小值.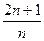
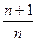
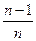
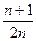
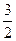 n2+
n2+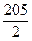 n,求数列{an}的通项公式.
n,求数列{an}的通项公式.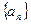 中,前
中,前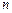 项和为
项和为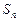 .已知
.已知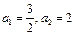 且
且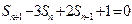 (
(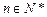 , 且
, 且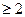 ).(1)求数列
).(1)求数列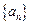 的通项公式;(2)求数列
的通项公式;(2)求数列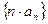 的前
的前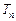 .
.