题目内容
含2n+1项的等差数列,其奇数项的和与偶数项的和之比为( )
A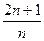． | B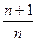． | C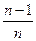． | D． |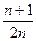
B
法一:设原数列为a1,a2,a3,…，a2n+1,公差为d,则a1,a3,a5, …，a2n+1和a2,a4,a6, …，a2n分别也为等差数列,公差都为2d.
故S奇=a1+a3+a5+…+a2n+1
=(n+1)a1+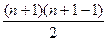
·2d=(n+1)(a1+nd).
S偶=a2+a4+a6+…+a2n=na1+
·2d=n(a1+nd).
∴
=
=.
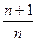∴应选B.
法二:∵S奇=a1+a3+a5+…+a2n+1=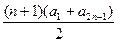
,
S偶=a2+a4+a6+…+a2n=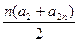
，
又∵a1+a2n+1=a2+a2n,
∴=.
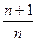∴应选B.
法三:取满足条件的等差数列:1,2,3,公差为1,且S奇=a1+a3=1+3=4,
S偶=a2=2.
∴=
=2=
.
∴应选B.
故S奇=a1+a3+a5+…+a2n+1
=(n+1)a1+
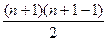·2d=(n+1)(a1+nd).S偶=a2+a4+a6+…+a2n=na1+
·2d=n(a1+nd).∴
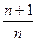==.∴应选B.
法二:∵S奇=a1+a3+a5+…+a2n+1=
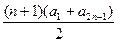,S偶=a2+a4+a6+…+a2n=
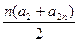，又∵a1+a2n+1=a2+a2n,
∴
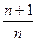=.∴应选B.
法三:取满足条件的等差数列:1,2,3,公差为1,且S奇=a1+a3=1+3=4,
S偶=a2=2.
∴
==2=.∴应选B.
练习册系列答案
相关题目
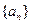的前
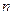项和为
，
（
）．
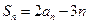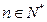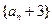是等比数列，求出数列
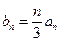，求数列
的前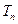
；
； 
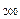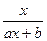(a、b为常数,a≠0)满足f(2)=1,且f(x)=x有唯一解。如记xn=f(xn-1),且x1=1,n∈N*,求xn.